Advertisements
Advertisements
प्रश्न
If from an external point B of a circle with centre O, two tangents BC and BD are drawn such that ∠DBC = 120°, prove that BC + BD = BO, i.e., BO = 2BC.
उत्तर

To prove: BO = 2BC
Given, ∠DBC = 120°
Join OC, OD and BO.
Since, BC and BD are tangents.
∴ OC ⊥ BC and OD ⊥ BD
We know, OB is the angle bisector of ∠DBC.
∴ ∠OBC = ∠DBO = 60°
In right-angled ∆OBC,
cos 60° = `("BC")/("OB")`
⇒ `1/2 = ("BC")/("OB")`
⇒ OB = 2 BC
Also, BC = BD ...[Tangent drawn from external point to circle are equal]
OB = BC + BC
⇒ OB = BC + BD
APPEARS IN
संबंधित प्रश्न
Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
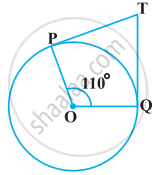
In the given figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to ______.
Prove that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.
Find the area of the shaded region in Fig. 8, where \\

In Figure 1, a quadrilateral ABCD is drawn to circumscribe a circle such that its sides AB, BC, CD and AD touch the circle at P, Q, R and S respectively. If AB = x cm, BC = 7 cm, CR = 3 cm and AS = 5 cm, find x.

(A) 10
(B) 9
(C) 8
(D) 7
M and N are the midpoints of chords AB and CD . The line MN passes through the centre O . Prove that AB || CD.
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.

Find: ∠AOB
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
PA and PB are tangents drawn to the circle with centre O as shown in the figure. Prove that ∠APB = 2∠OAB.

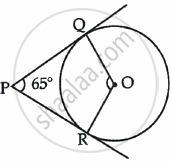
In the given figure, PQ and PR are tangents drawn from P to the circle with centre O such that ∠QPR = 65°. The measure of ∠QOR is ______.