Advertisements
Advertisements
प्रश्न
Prove that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.
उत्तर
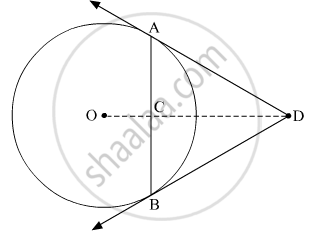
Let AB be a chord of a circle with centre O, and let AD and BD be the tangents at A and B respectively.
Suppose OD meets AB at C.
We have to prove that ∠DAC = ∠DBC.
We know that, the line segment joining the centre to the external point, bisects the angle between two tangents.
So, ∠ADC=∠BDC ...(i)
In △DCA and △DCB, we have
DA = DB [Tangents from an external point are equal]
∠ADC = ∠BDC [From (i)]
DC=DC [Common]
∴ ∆DCA ≅ ∆DCB [By SAS congruency rule]
⇒∠DAC = ∠DBC [BY C.P.CT]
APPEARS IN
संबंधित प्रश्न
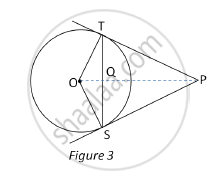
In Fig.3, from an external point P, two tangents PT and PS are drawn to a circle with centre O and radius r. If OP = 2r, show that ∠ OTS = ∠ OST = 30°.
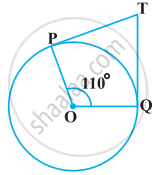
In the given figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to ______.
Two concentric circles are of radii 5 cm and 3 cm. Length of the chord of the larger circle, (in cm), which touches the smaller circle is
(A) 4
(B) 5
(C) 8
(D) 10
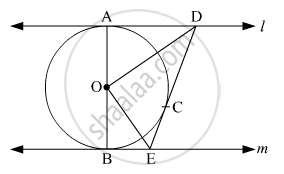
In fig. 6, l and m are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that ∠DOE = 90° ?
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
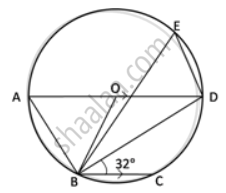
Find: ∠BED
The number of tangents drawn at a point of the circle is/are ______
Draw two concentric circles of radii 2 cm and 3 cm. From a point on the outer circle, construct a pair of tangents to the inner circle.
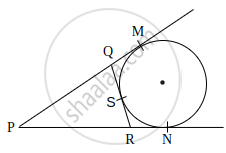
In the given figure, if a circle touches the side QR of ΔPQR at S and extended sides PQ and PR at M and N, respectively, then prove that PM = `1/2` (PQ + QR + PR)
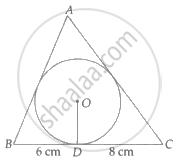
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 6 cm and 8 cm respectively. If the area of ΔABC is 84 cm2, find the lengths of sides AB and AC.
In the given figure, BC is tangent to the circle at point B of circle centred at O. BD is a chord of the circle so that ∠BAD = 55°. Find m∠DBC.

