Advertisements
Advertisements
प्रश्न
Two concentric circles are of radii 5 cm and 3 cm. Length of the chord of the larger circle, (in cm), which touches the smaller circle is
(A) 4
(B) 5
(C) 8
(D) 10
उत्तर
Let O be the centre of the concentric circles.
Let AB be the chord of the larger circle touching the smaller circle at C.
Also, let OC and OB be the radii of the smaller circle and the larger circle, respectively.
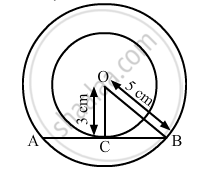
We can see that AB is the tangent to the smaller circle.
We know that the tangent at any point on a circle is perpendicular to the radius drawn to the point of contact.
∴ OC ⊥ AB
Now, in the right-angled triangle OCB:
OB2 = OC2 + CB2 (Pythagoras theorem)
⇒ CB2 = {(5)2 − (3)2} cm2
= (25 − 9) cm2
= 16 cm2
⇒ CB = 4 cm
Now, AB = 2(CB) (The perpendicular from the centre of the circle to the chord bisects the chord.)
⇒ AB = 8 cm
Hence, the correct option is C.
APPEARS IN
संबंधित प्रश्न
In the below given figure, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If∠PRQ = 120°, then prove that OR = PR + RQ.

From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is ______.
In the given circle with center o, ∠ABC=100°, ∠ACD=40° and CT is tangent to the circle at C. find ∠ADC and ∠DCT.

In the given figure, PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ = 30°, prove that : BD is diameter of the circle.
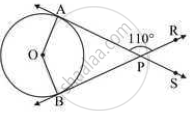
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 110°.
The length of the tangent from an external point P on a circle with centre O is ______
In a circle of radius 5 cm, AB and AC are the two chords such that AB = AC = 6 cm. Find the length of the chord BC.
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the center O at a point Q such that OQ = 13 cm. Length PQ is ______
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 90°, then OP = `asqrt(2)`.
In the given figure, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q meet at a point T. Find the length of TP.

