Advertisements
Advertisements
प्रश्न
In the given figure, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q meet at a point T. Find the length of TP.

उत्तर
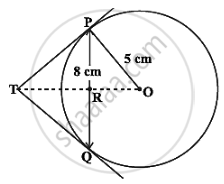
We know that tangents from an external point are equal in length, therefore TP = TQ
⇒ ΔTPQ is an isosceles triangle.
Also, we know that tangents from the external points are equally inclined to the segment.
∴ OT is bisector of ∠PTQ
⇒ OT ⊥ PQ ....[∵ In an isosceles triangle, angle bisector and altitude are the same]
⇒ ∠ORP = ∠TRP = 90°
Now, In ΔORP,
OR = `sqrt(5^2 - "PR"^2)`
= `sqrt(25 - 4^2)` .....[∵ Perpendicular from centre to a chord bisect the chord and so PR = RQ = 4 cm]
= `sqrt(25 - 16)`
= 3 cm
∵ ∠OPT = 90 .....[∵ Radius is ⊥ to the tangent at the point of contact]
∴ TP2 = OT2 – OP2 = (TR + 3)2 – 52 ...(i)
Also, from ΔPRT,
TP2 = PR2 + TR2 = 42 + TR2 ...(ii)
From equations (i) and (ii), we get
(TR + 3)2 – 52 = 42 + TR2
⇒ TR2 + 9 + 6TR – TR2 = 25 + 16 = 41
⇒ 6TR = 41 – 9 = 32
⇒ TR = `16/3`
Now, from equation (ii), we get
TP2 = `4^2 + (16/3)^2`
= `(16 xx 9 + 256)/9`
= `(144 + 256)/9`
= `400/9`
= `20/3`
TP = 6.67 cm
APPEARS IN
संबंधित प्रश्न
Prove that “The lengths of the two tangent segments to a circle drawn from an external point are equal.”
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact to the centre.
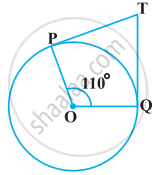
In the given figure, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to ______.
If tangents PA and PB from a point P to a circle with centre O are inclined to each other an angle of 80°, then ∠POA is equal to ______.
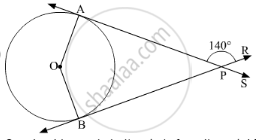
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 140°.
Find the area of the shaded region in Fig. 8, where \\

In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.

Find: ∠AOB
In the given figure, ▢ABCD is a parallelogram. It circumscribes the circle with centre T. Point E, F, G, H are touching points. If AE = 4.5, EB = 5.5, find AD.

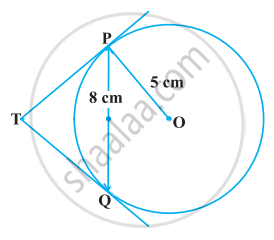
ln Figure, PQ is a chord of length 8 cm of a circle of radius 5 cm and centre O. The tangents at P and Q intersect at point T. find the length of TP.
In the given figure, perimeter of ΔPQR is 20 cm. Find the length of tangent PA.

