Advertisements
Advertisements
प्रश्न
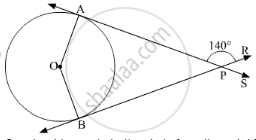
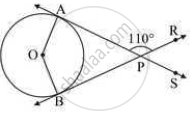
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 140°.
उत्तर
\[ \Rightarrow \angle APB = 40^o\]
Also,
\[\angle\]OAP =
\[ \Rightarrow 40^o + 90^o + \angle BOA + 90^o = 360^o\]
\[ \Rightarrow \angle BOA = 140^o\]
APPEARS IN
संबंधित प्रश्न
Prove that “The lengths of the two tangent segments to a circle drawn from an external point are equal.”
In the following figure, Q is the centre of a circle and PM, PN are tangent segments to the circle. If ∠MPN = 50°, find ∠MQN.

Prove that the lengths of the tangents drawn from an external point to a circle are equal.
Prove that a parallelogram circumscribing a circle is a rhombus.
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segments joining the points of contact to the centre.
Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
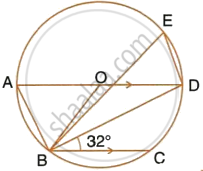
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°.
Find:
- ∠OBD
- ∠AOB
- ∠BED
Find the area of the shaded region in Fig. 8, where \\

Two concentric circles are of radii 5 cm and 3 cm. Length of the chord of the larger circle, (in cm), which touches the smaller circle is
(A) 4
(B) 5
(C) 8
(D) 10
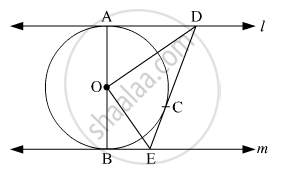
In fig. 6, l and m are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that ∠DOE = 90° ?
In the given figure, PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ = 30°, prove that : BD is diameter of the circle.
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 110°.
In the given figure, ▢ABCD is a parallelogram. It circumscribes the circle with centre T. Point E, F, G, H are touching points. If AE = 4.5, EB = 5.5, find AD.

A tangent is drawn from a point at a distance of 17 cm of circle C(0, r) of radius 8 cm. The length of its tangent is ______
The angle between two tangents to a circle may be 0°.
In figure, common tangents AB and CD to two circles intersect at E. Prove that AB = CD.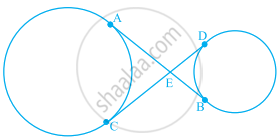
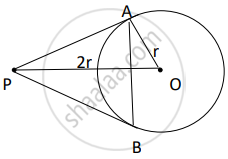
From a point P, two tangents PA and PB are drawn to a circle C(0, r). If OP = 2r, then find ∠APB. What type of triangle is APB?
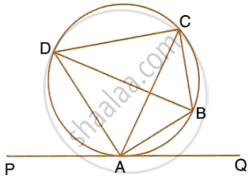
In the given figure, there are two concentric circles with centre O. If ARC and AQB are tangents to the smaller circle from the point A lying on the larger circle, find the length of AC, if AQ = 5 cm.

