Advertisements
Advertisements
प्रश्न
Prove that “The lengths of the two tangent segments to a circle drawn from an external point are equal.”
उत्तर १
Given: A circle with centre O and an external point P are given.
AP and BP are the two tangents drawn from an external point P.

To prove: AP = BP
Construction: Draw seg OA, seg OB and seg OP.
Proof: In ΔOBP and ΔOAP,
OA = OB … (Radii of the same circle)
OP = OP … (Side common to both the triangles)
∠OAP = ∠OBP = 90° … (tangent is perpendicular to the radius at the point of contact)
ΔOBP ≅ ΔOAP … (By R.H.S)
∴ AP = BP … (corresponding sides of congruent triangles)
Thus, the lengths of two tangent segments to a circle drawn from an external point are equal.
उत्तर २
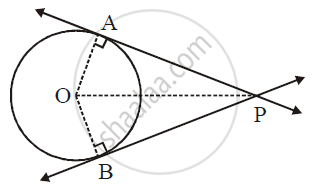
Given: O is the centre of the circle and P is a point in the exterior of the circle. A and B are the points of contact of the two tangents from P to the circle.
To Prove: PA = PB
Construction: Draw seg OA, seg OB and seg OP.
Proof: Line AP ⊥ radius OA and line BP ⊥ radius OB ... (Tangent perpendicular to radius)
∴ `anglePAO = anglePBO = 90^@`
In right-angled triangles `triangle OAP` and `triangleOBP`
hypotenuse OP ≅ hypotenuse OP ...(Common side)
seg OA ≅ seg OB ...(Radii of the same circle)
`:.triangleOAP ≅ triangleOBP` ...(Hypotenuse-side of theorem)
∴ seg PA ≅ seg PB ...(c.s.c.t.)
∴ PA = PB
APPEARS IN
संबंधित प्रश्न
From an external point P, tangents PA and PB are drawn to a circle with centre O. If ∠PAB = 50°, then find ∠AOB.
Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
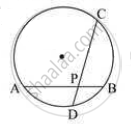
In the given figure PA = 10, PB = 2 and PC = 5. Find PD.
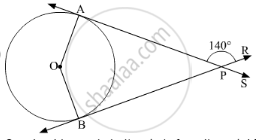
Find the angle between two radii at the centre of the circle as shown in the figure. Lines PA and PB are tangents to the circle at other ends of the radii and ∠APR = 140°.
PQ is a tangent drawn from an external point P to a circle with centre O, QOR is the diameter of the circle. If ∠POR = 120°, what is the measure of ∠OPQ?
In the given circle with center o, ∠ABC=100°, ∠ACD=40° and CT is tangent to the circle at C. find ∠ADC and ∠DCT.

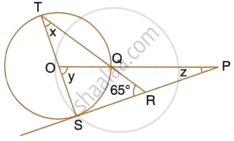
In the figure given below, O is the center of the circle and SP is a tangent. If ∠SRT = 65°, find the value of x, y and Z.
M and N are the midpoints of chords AB and CD . The line MN passes through the centre O . Prove that AB || CD.
In the given figure PA = 6, PB = 4 and PC = 8. Find PD
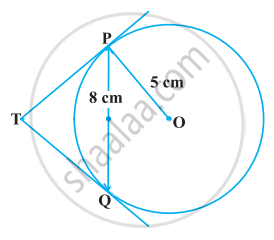
ln Figure, PQ is a chord of length 8 cm of a circle of radius 5 cm and centre O. The tangents at P and Q intersect at point T. find the length of TP.
Prove that the lengths of two tangent segments drawn to the circle from an external point are equal.
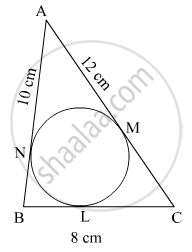
In Fig. 4, a circle is inscribed in a ΔABC having sides BC = 8 cm, AB = 10 cm and AC = 12 cm. Find the lengths BL, CM and AN.
Two concentric circles of radii a and b (a > b) are given. Find the length of the chord of the larger circle which touches the smaller circle.
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the center O at a point Q such that OQ = 13 cm. Length PQ is ______
The angle between two tangents to a circle may be 0°.
In the given figure, O is the centre of circle. Find ∠AQB, given that PA and PB are tangents to the circle and ∠APB = 75°.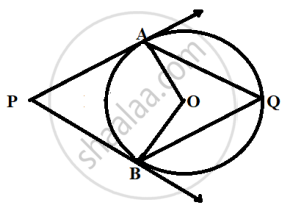
Draw two concentric circles of radii 2 cm and 3 cm. From a point on the outer circle, construct a pair of tangents to the inner circle.
In the given figure, PA and PB are tangents from external point P to a circle with centre C and Q is any point on the circle. Then the measure of ∠AQB is ______.

Two concentric circles with centre O are of radii 3 cm and 5 cm. Find the length of chord AB of the larger circle which touches the smaller circle at P.

PA and PB are tangents drawn to the circle with centre O as shown in the figure. Prove that ∠APB = 2∠OAB.

