Advertisements
Advertisements
प्रश्न
Write the equation of the line passing through the pair of points (2, 3) and (4, 7) in the form of y = mx + c.
उत्तर
Let (2, 3) ≡ (x1, y1) and (4, 7) ≡ (x2, y2).
The equation of a line passing through a pair of points is
m = `("y"_2 - "y"_1)/("x"_2 - "x"_1)`
`= (7-3)/(4-2) = 4/2 = 2`
Here, I have two points, which I used to find the slope. Now I need to pick one of the points (it doesn't matter which one), and use it to solve for b
Using the point (2,3), I get :
y = mx + b
3 = 2(2) + b
3 = 4 + b
3 - 4 = b
b = -1
So , y = 2x - 1
On the other hand, if I use the point (4,7), I get:
y = mx + b
7 = 2(4) + b
7 = 8 + b
7 - 8 = b
b = -1
then y = 2x - 1
So it doesn't matter which point I choose. Either way, the answer is the same : y = 2x - 1
APPEARS IN
संबंधित प्रश्न
A (5, 4), B (-3, -2) and C (1, -8) are the vertices of a triangle ABC. Find the equations of the median AD and line parallel to AC passing through the point B.
Find the slope and y-intercept of the line:
y = 4
Find the slope and y-intercept of the line:
3x – 4y = 5
Is the line 3x + 4y + 7 = 0 perpendicular to the line 28x – 21y + 50 = 0?
Is the line 3x + 2y = 5 parallel to the line x + 2y = 1?
B(−5, 6) and D(1, 4) are the vertices of rhombus ABCD. Find the equations of diagonals BD and AC.
Find the equation of the line which is perpendicular to the line `x/a - y/b = 1` at the point where this line meets y-axis.
Find the point on the X–axis which is equidistant from A(–3, 4) and B(1, –4).
Verify that points P(–2, 2), Q(2, 2) and R(2, 7) are vertices of a right angled triangle.
Show that points P(2, –2), Q(7, 3), R(11, –1) and S (6, –6) are vertices of a parallelogram.
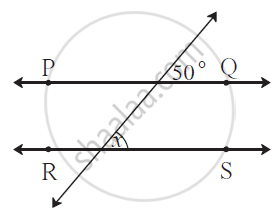
In the figure, line PQ || line RS. Using the information given
in the figure find the value of x.
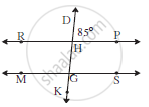
In the adjoining figure line RP ||line MS , line DK is a transversal . If ∠DHP = 85° find ∠RHG and ∠HGS.
Line PQ is parallel to line RS where points P,Q,R and S have
co-ordinates (2, 4), (3, 6), (3, 1) and (5, k) respectively. Find value of k.
Find:
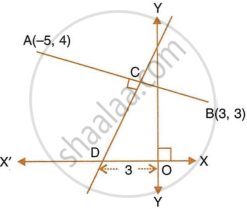
- equation of AB
- equation of CD
A line is parallel to Y-axis and is at a distance of 5 units from the Y-axis. Write the equation of that line.
