Advertisements
Advertisements
प्रश्न
Write the equation of the line passing through the pair of points (2, 3) and (4, 7) in the form of y = mx + c.
उत्तर
Let (2, 3) ≡ (x1, y1) and (4, 7) ≡ (x2, y2).
The equation of a line passing through a pair of points is
m = `("y"_2 - "y"_1)/("x"_2 - "x"_1)`
`= (7-3)/(4-2) = 4/2 = 2`
Here, I have two points, which I used to find the slope. Now I need to pick one of the points (it doesn't matter which one), and use it to solve for b
Using the point (2,3), I get :
y = mx + b
3 = 2(2) + b
3 = 4 + b
3 - 4 = b
b = -1
So , y = 2x - 1
On the other hand, if I use the point (4,7), I get:
y = mx + b
7 = 2(4) + b
7 = 8 + b
7 - 8 = b
b = -1
then y = 2x - 1
So it doesn't matter which point I choose. Either way, the answer is the same : y = 2x - 1
APPEARS IN
संबंधित प्रश्न
Write the equation of each of the following lines:
- The x-axis and the y-axis.
- The line passing through the origin and the point (-3, 5).
- The line passing through the point (-3, 4) and parallel to X-axis.
In ΔABC, A(3, 5), B(7, 8) and C(1, –10). Find the equation of the median through A.
Find the slope and y-intercept of the line:
y = 4
Find the slope and y-intercept of the line:
ax – by = 0
The equation of a line is x – y = 4. Find its slope and y-intercept. Also, find its inclination.
Is the line 3x + 2y = 5 parallel to the line x + 2y = 1?
Find the equation of the line passing through (−2, 1) and perpendicular to 4x + 5y = 6.
A = (7, −2) and C = (−1, −6) are the vertices of square ABCD. Find the equations of diagonals AC and BD.
A (5, 4), B (–3,–2) and C (1,–8) are the vertices of a triangle ABC. Find the equation of median AD and line parallel to AB passing through point C.
Find the point on the X–axis which is equidistant from A(–3, 4) and B(1, –4).
Verify that points P(–2, 2), Q(2, 2) and R(2, 7) are vertices of a right angled triangle.
Show that points P(2, –2), Q(7, 3), R(11, –1) and S (6, –6) are vertices of a parallelogram.
Line PQ is parallel to line RS where points P,Q,R and S have
co-ordinates (2, 4), (3, 6), (3, 1) and (5, k) respectively. Find value of k.
Find:
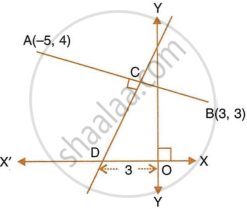
- equation of AB
- equation of CD
A line through point P(4, 3) meets x-axis at point A and the y-axis at point B. If BP is double of PA, find the equation of AB.
Find the equation of the line through the points A(–1, 3) and B(0, 2). Hence, show that the point A, B and C(1, 1) are collinear.
If (4,-3) is a point on line 5x +8y = c, find the value of c.
A line is parallel to Y-axis and is at a distance of 5 units from the Y-axis. Write the equation of that line.
