Advertisements
Advertisements
प्रश्न
Show that points P(2, –2), Q(7, 3), R(11, –1) and S (6, –6) are vertices of a parallelogram.
उत्तर
The given points are P(2, –2), Q(7, 3), R(11, –1) and S(6, –6).
`"Distance between" = sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)`
By distance formula,
PQ = `sqrt((7 - 2)^2 + [3 - ( - 2)]^2)`
∴ PQ = `sqrt((7 - 2)^2 + (3 + 2)^2)`
∴ PQ = `sqrt((5)^2 + (5)^2)`
∴ PQ = `sqrt(25 + 25)`
∴ PQ = `sqrt(50)`
∴ PQ = `sqrt(25 × 2)`
∴ PQ = `5sqrt(2)` ...(1)
QR = `sqrt((11 - 7)^2 + (-1 - 3)^2)`
∴ QR = `sqrt((4)^2 + (-4)^2)`
∴ QR = `sqrt(16 + 16)`
∴ QR = `sqrt(32)`
∴ QR = `sqrt(16 × 2)`
∴ QR = `4sqrt(2)` ...(2)
RS = `sqrt((6 - 11)^2 + [-6 - (- 1)]^2)`
∴ RS = `sqrt((- 5)^2 + (-6 + 1)^2)`
∴ RS = `sqrt((- 5)^2 + (-5)^2)`
∴ RS = `sqrt(25 + 25)`
∴ RS = `sqrt(50)`
∴ RS = `sqrt(25 × 2)`
∴ RS = `5sqrt(2)` ...(3)
PS = `sqrt((6 - 2)^2 + [-6 - (- 2)]^2)`
∴ PS = `sqrt((6 - 2)^2 + [-6 + 2]^2)`
∴ PS = `sqrt((4)^2 + (-4)^2)`
∴ PS = `sqrt(16 + 16)`
∴ PS = `sqrt(32)`
∴ PS = `sqrt(16 × 2)`
∴ PS = `4sqrt(2)` ...(4)
In □ PQRS,
PQ = RS ...[From (1) and (3)]
QR = PS ...[From (2) and (4)]
A quadrilateral is a parallelogram, if both the pairs of its opposite sides are congruent.
Checking for slopes,
Slope of a line between two points (x1, y1) and (x2, y2) is
m = `(y_2 - y_1)/(x_2 - x_1)`
Slope PQ = `(7 - 2)/[3 - (- 2)] = 1`
Slope QR = `(11 - 7)/[- 1 - 3] = - 1`
Slope RS = `(6 - 11)/[- 6 - (- 1)] = 1`
Slope SP = `(6 - 2)/[- 6 - (- 2)] = - 1`
As PQ = RS and their slope = 1 And QR = SP and their slope = -1.
∴ □ PQRS is parallelogram.
∴ P, Q, R, and S are vertices of a parallelogram.
APPEARS IN
संबंधित प्रश्न
Write the equation of the line passing through the pair of points (2, 3) and (4, 7) in the form of y = mx + c.
A (5, 4), B (-3, -2) and C (1, -8) are the vertices of a triangle ABC. Find the equations of the median AD and line parallel to AC passing through the point B.
In ΔABC, A(3, 5), B(7, 8) and C(1, –10). Find the equation of the median through A.
Find the slope and y-intercept of the line:
3x – 4y = 5
The equation of a line is x – y = 4. Find its slope and y-intercept. Also, find its inclination.
Is the line 3x + 2y = 5 parallel to the line x + 2y = 1?
B(−5, 6) and D(1, 4) are the vertices of rhombus ABCD. Find the equations of diagonals BD and AC.
A = (7, −2) and C = (−1, −6) are the vertices of square ABCD. Find the equations of diagonals AC and BD.
- Write down the equation of the line AB, through (3, 2) and perpendicular to the line 2y = 3x + 5.
- AB meets the x-axis at A and the y-axis at B. Write down the co-ordinates of A and B. Calculate the area of triangle OAB, where O is the origin.
Find the point on the X–axis which is equidistant from A(–3, 4) and B(1, –4).
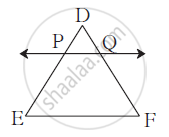
In Δ DEF, line PQ || side EF, If DP = 2.4,
PE = 7.2, DQ = 1 then find QF.
Prove that :
“If a line parallel to a side of a triangle intersects the remaining sides in two distince points, then the line divides the sides in the same proportion.”
Find the equation of the line that has x-intercept = –3 and is perpendicular to 3x + 5y = 1.
A straight line passes through the points P(–1, 4) and Q(5, –2). It intersects x-axis at point A and y-axis at point B. M is the mid-point of the line segment AB. Find:
- the equation of the line.
- the co-ordinates of point A and B.
- the co-ordinates of point M.
In the given figure, line AB meets y-axis at point A. Line through C(2, 10) and D intersects line AB at right angle at point P. Find:
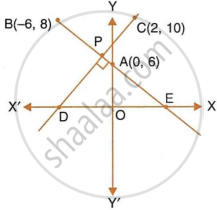
- equation of line AB.
- equation of line CD.
- co-ordinates of points E and D.
Three vertices of a parallelogram ABCD taken in order are A(3, 6), B(5, 10) and C(3, 2), find:
- the co-ordinates of the fourth vertex D.
- length of diagonal BD.
- equation of side AB of the parallelogram ABCD.
In the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
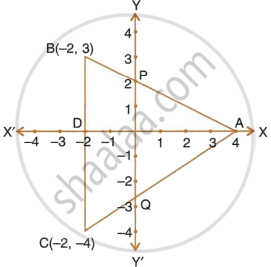
- Write the co-ordinates of A.
- Find the length of AB and AC.
- Find the radio in which Q divides AC.
- Find the equation of the line AC.
A line is parallel to Y-axis and is at a distance of 5 units from the Y-axis. Write the equation of that line.
