Advertisements
Advertisements
प्रश्न
- Write down the equation of the line AB, through (3, 2) and perpendicular to the line 2y = 3x + 5.
- AB meets the x-axis at A and the y-axis at B. Write down the co-ordinates of A and B. Calculate the area of triangle OAB, where O is the origin.
उत्तर
i. 2y = 3x + 5
`=> y = (3x)/2 + 5/2`
Slope of this line = `3/2`
Slope of the line AB = `(-1)/(3/2) = (-2)/3`
(x1, y1) = (3, 2)
The required equation of the line AB is
y − y1 = m(x − x1)
`y - 2 = (-2)/3 (x - 3)`
3y − 6 = −2x + 6
2x + 3y = 12
ii. For the point A (the point on x-axis), the value of y = 0.
2x + 3y = 12
`=>` 2x = 12
`=>` x = 6
Co-ordinates of point A are (6, 0).
For the point B (the point on y-axis), the value of x = 0.
2x + 3y = 12
`=>` 3y = 12
`=>` y = 4
Co-ordinates of point B are (0, 4).
Area of ΔOAB = `1/2 xx OA xx OB`
= `1/2 xx 6 xx 4`
= 12 sq units
APPEARS IN
संबंधित प्रश्न
Find the slope and y-intercept of the line:
3x – 4y = 5
Is the line 3x + 4y + 7 = 0 perpendicular to the line 28x – 21y + 50 = 0?
Is the line x – 3y = 4 perpendicular to the line 3x – y = 7?
Is the line 3x + 2y = 5 parallel to the line x + 2y = 1?
The point P is the foot of perpendicular from A(−5, 7) to the line whose equation is 2x – 3y + 18 = 0. Determine :
- the equation of the line AP.
- the co-ordinates of P.
Find the point on the X–axis which is equidistant from A(–3, 4) and B(1, –4).
Verify that points P(–2, 2), Q(2, 2) and R(2, 7) are vertices of a right angled triangle.
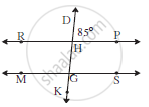
In the adjoining figure line RP ||line MS , line DK is a transversal . If ∠DHP = 85° find ∠RHG and ∠HGS.
Find the equation of the line through the points A(–1, 3) and B(0, 2). Hence, show that the point A, B and C(1, 1) are collinear.
Three vertices of a parallelogram ABCD taken in order are A(3, 6), B(5, 10) and C(3, 2), find:
- the co-ordinates of the fourth vertex D.
- length of diagonal BD.
- equation of side AB of the parallelogram ABCD.
