Advertisements
Advertisements
प्रश्न
In ΔABC, A(3, 5), B(7, 8) and C(1, –10). Find the equation of the median through A.
उत्तर
The vertices of ΔABC are A(3, 5), B(7, 8) and C(1, –10).
Coordinates of the mid-point D of BC =
`((7 + 1)/2, (8 - 10)/2) = (8/2, (-2)/2) = (4, -1)`
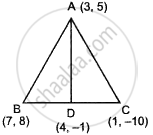
Slope of AD = `(y_2 - y_1)/(x_2 - x_1)`
= `(-1 - 5)/(4 - 3)`
= `(-6)/1`
Slope of AD = – 6
Now, the equation of median AD is given by
y – y1 = m(x – x1)
∴ y – 5 = – 6(x – 3)
∴ y – 5 = – 6x + 18
∴ 6x + y – 5 – 18 = 0
∴ 6x + y – 23 = 0
संबंधित प्रश्न
A (5, 4), B (-3, -2) and C (1, -8) are the vertices of a triangle ABC. Find the equations of the median AD and line parallel to AC passing through the point B.
If (4,-3) is a point on the line AB and slope of the line is (-2), write the equation of the line AB.
Write the equation of each of the following lines:
- The x-axis and the y-axis.
- The line passing through the origin and the point (-3, 5).
- The line passing through the point (-3, 4) and parallel to X-axis.
Find the slope and y-intercept of the line:
ax – by = 0
Is the line 3x + 2y = 5 parallel to the line x + 2y = 1?
The points A, B and C are (4, 0), (2, 2) and (0, 6) respectively. Find the equations of AB and BC. If AB cuts the y-axis at P and BC cuts the x-axis at Q, find the co-ordinates of P and Q.
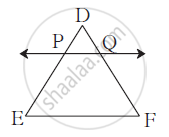
In Δ DEF, line PQ || side EF, If DP = 2.4,
PE = 7.2, DQ = 1 then find QF.
Prove that :
“If a line parallel to a side of a triangle intersects the remaining sides in two distince points, then the line divides the sides in the same proportion.”
A straight line passes through the points P(–1, 4) and Q(5, –2). It intersects x-axis at point A and y-axis at point B. M is the mid-point of the line segment AB. Find:
- the equation of the line.
- the co-ordinates of point A and B.
- the co-ordinates of point M.
A line through point P(4, 3) meets x-axis at point A and the y-axis at point B. If BP is double of PA, find the equation of AB.
