Advertisements
Advertisements
प्रश्न
If (4,-3) is a point on the line AB and slope of the line is (-2), write the equation of the line AB.
उत्तर
(4, -3) ≡ (x1, y1) is a point on the line AB and slope = m = -2
Equation of line AB in point slope form is
y - y1 = m(x - x1)
y - (-3) = -2(x - 4)
y + 3 = -2x + 8
2x + y - 5 = 0
APPEARS IN
संबंधित प्रश्न
Write the equation of the line passing through the pair of points (2, 3) and (4, 7) in the form of y = mx + c.
Write the equation of each of the following lines:
- The x-axis and the y-axis.
- The line passing through the origin and the point (-3, 5).
- The line passing through the point (-3, 4) and parallel to X-axis.
In ΔABC, A(3, 5), B(7, 8) and C(1, –10). Find the equation of the median through A.
Find the slope and y-intercept of the line:
y = 4
Is the line x – 3y = 4 perpendicular to the line 3x – y = 7?
Find the equation of the perpendicular bisector of the line segment obtained on joining the points (6, −3) and (0, 3).
The line 4x − 3y + 12 = 0 meets x-axis at A. Write the co-ordinates of A. Determine the equation of the line through A and perpendicular to 4x – 3y + 12 = 0.
The point P is the foot of perpendicular from A(−5, 7) to the line whose equation is 2x – 3y + 18 = 0. Determine :
- the equation of the line AP.
- the co-ordinates of P.
The points A, B and C are (4, 0), (2, 2) and (0, 6) respectively. Find the equations of AB and BC. If AB cuts the y-axis at P and BC cuts the x-axis at Q, find the co-ordinates of P and Q.
Find the point on the X–axis which is equidistant from A(–3, 4) and B(1, –4).
Verify that points P(–2, 2), Q(2, 2) and R(2, 7) are vertices of a right angled triangle.
Show that points P(2, –2), Q(7, 3), R(11, –1) and S (6, –6) are vertices of a parallelogram.
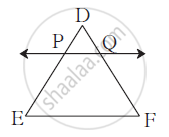
In Δ DEF, line PQ || side EF, If DP = 2.4,
PE = 7.2, DQ = 1 then find QF.
Find Equation of CD
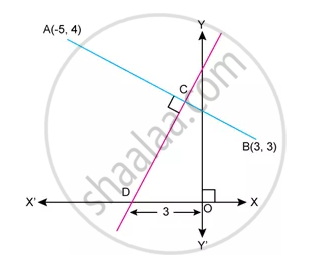
In the given figure, line AB meets y-axis at point A. Line through C(2, 10) and D intersects line AB at right angle at point P. Find:
- equation of line AB.
- equation of line CD.
- co-ordinates of points E and D.
Find the equation of the line through the points A(–1, 3) and B(0, 2). Hence, show that the point A, B and C(1, 1) are collinear.
Three vertices of a parallelogram ABCD taken in order are A(3, 6), B(5, 10) and C(3, 2), find:
- the co-ordinates of the fourth vertex D.
- length of diagonal BD.
- equation of side AB of the parallelogram ABCD.
In the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
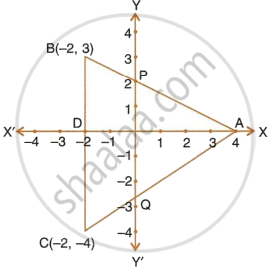
- Write the co-ordinates of A.
- Find the length of AB and AC.
- Find the radio in which Q divides AC.
- Find the equation of the line AC.
A line segment joining P(2, –3) and Q(0, –1) is cut by the x-axis at the point R. A line AB cuts the y-axis at T(0, 6) and is perpendicular to PQ at S.
Find the:
- equation of line PQ
- equation of line AB
- coordinates of points R and S.
