Advertisements
Advertisements
प्रश्न
If (4,-3) is a point on the line AB and slope of the line is (-2), write the equation of the line AB.
उत्तर
(4, -3) ≡ (x1, y1) is a point on the line AB and slope = m = -2
Equation of line AB in point slope form is
y - y1 = m(x - x1)
y - (-3) = -2(x - 4)
y + 3 = -2x + 8
2x + y - 5 = 0
APPEARS IN
संबंधित प्रश्न
Write the equation of each of the following lines:
- The x-axis and the y-axis.
- The line passing through the origin and the point (-3, 5).
- The line passing through the point (-3, 4) and parallel to X-axis.
Given 3x + 2y + 4 = 0
(i) express the equation in the form y = mx + c
(ii) Find the slope and y-intercept of the line 3x + 2y + 4 = 0
Find the slope and y-intercept of the line:
y = 4
Find the slope and y-intercept of the line:
ax – by = 0
The equation of a line is x – y = 4. Find its slope and y-intercept. Also, find its inclination.
Is the line 3x + 4y + 7 = 0 perpendicular to the line 28x – 21y + 50 = 0?
Is the line 3x + 2y = 5 parallel to the line x + 2y = 1?
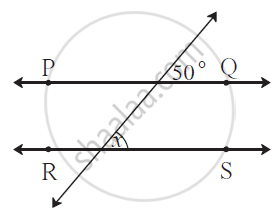
In the figure, line PQ || line RS. Using the information given
in the figure find the value of x.
Line PQ is parallel to line RS where points P,Q,R and S have
co-ordinates (2, 4), (3, 6), (3, 1) and (5, k) respectively. Find value of k.
Find:
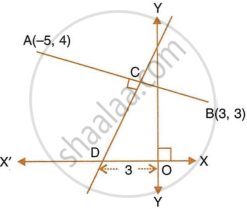
- equation of AB
- equation of CD
Find Equation of CD
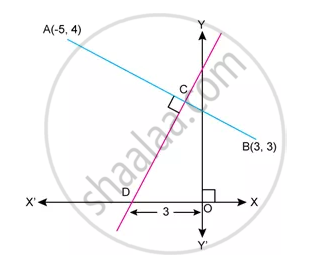
Find the equation of the line that has x-intercept = –3 and is perpendicular to 3x + 5y = 1.
Find the equation of line through the intersection of lines 2x – y = 1 and 3x + 2y = –9 and making an angle of 30° with positive direction of x-axis.
Three vertices of a parallelogram ABCD taken in order are A(3, 6), B(5, 10) and C(3, 2), find:
- the co-ordinates of the fourth vertex D.
- length of diagonal BD.
- equation of side AB of the parallelogram ABCD.
In the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
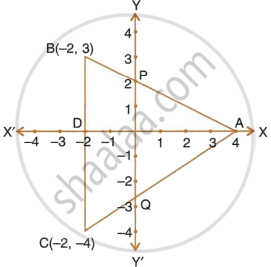
- Write the co-ordinates of A.
- Find the length of AB and AC.
- Find the radio in which Q divides AC.
- Find the equation of the line AC.
If (4,-3) is a point on line 5x +8y = c, find the value of c.
Find the equation of the line passing through the points (4,-5) and (-1,-2).
