Advertisements
Advertisements
प्रश्न
Is the line 3x + 2y = 5 parallel to the line x + 2y = 1?
उत्तर
∴ 3x + 2y = 5
2y = −3x + 5
`y = (-3x)/2 + 5/2`
Slope of this line = `(-3)/2`
∴ x + 2y = 1
2y = −x + 1
`y = (-1x)/2 + 1/2`
Slope of this line = `(-1)/2`
Product of slopes of the two lines = `(-3)/2 ≠ (-1)/2`
So, the lines are not parallel to each other.
APPEARS IN
संबंधित प्रश्न
A (5, 4), B (-3, -2) and C (1, -8) are the vertices of a triangle ABC. Find the equations of the median AD and line parallel to AC passing through the point B.
If (4,-3) is a point on the line AB and slope of the line is (-2), write the equation of the line AB.
Find the slope and y-intercept of the line:
y = 4
Find the slope and y-intercept of the line:
ax – by = 0
Find the slope and y-intercept of the line:
3x – 4y = 5
B(−5, 6) and D(1, 4) are the vertices of rhombus ABCD. Find the equations of diagonals BD and AC.
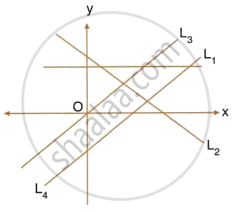
Match the equations A, B, C and D with the lines L1, L2, L3 and L4, whose graphs are roughly drawn in the given diagram.
A ≡ y = 2x;
B ≡ y – 2x + 2 = 0;
C ≡ 3x + 2y = 6;
D ≡ y = 2
Find the point on the X–axis which is equidistant from A(–3, 4) and B(1, –4).
Three vertices of a parallelogram ABCD taken in order are A(3, 6), B(5, 10) and C(3, 2), find:
- the co-ordinates of the fourth vertex D.
- length of diagonal BD.
- equation of side AB of the parallelogram ABCD.
A line is parallel to Y-axis and is at a distance of 5 units from the Y-axis. Write the equation of that line.
