Advertisements
Advertisements
प्रश्न
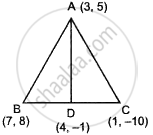
In ΔABC, A(3, 5), B(7, 8) and C(1, –10). Find the equation of the median through A.
उत्तर
The vertices of ΔABC are A(3, 5), B(7, 8) and C(1, –10).
Coordinates of the mid-point D of BC =
`((7 + 1)/2, (8 - 10)/2) = (8/2, (-2)/2) = (4, -1)`
Slope of AD = `(y_2 - y_1)/(x_2 - x_1)`
= `(-1 - 5)/(4 - 3)`
= `(-6)/1`
Slope of AD = – 6
Now, the equation of median AD is given by
y – y1 = m(x – x1)
∴ y – 5 = – 6(x – 3)
∴ y – 5 = – 6x + 18
∴ 6x + y – 5 – 18 = 0
∴ 6x + y – 23 = 0
संबंधित प्रश्न
If (4,-3) is a point on the line AB and slope of the line is (-2), write the equation of the line AB.
Given 3x + 2y + 4 = 0
(i) express the equation in the form y = mx + c
(ii) Find the slope and y-intercept of the line 3x + 2y + 4 = 0
Find the slope and y-intercept of the line:
y = 4
Is the line 3x + 4y + 7 = 0 perpendicular to the line 28x – 21y + 50 = 0?
Is the line 3x + 2y = 5 parallel to the line x + 2y = 1?
B(−5, 6) and D(1, 4) are the vertices of rhombus ABCD. Find the equations of diagonals BD and AC.
Verify that points P(–2, 2), Q(2, 2) and R(2, 7) are vertices of a right angled triangle.
Prove that :
“If a line parallel to a side of a triangle intersects the remaining sides in two distince points, then the line divides the sides in the same proportion.”
Find Equation of CD
Find the equation of the line through the points A(–1, 3) and B(0, 2). Hence, show that the point A, B and C(1, 1) are collinear.
