Advertisements
Advertisements
प्रश्न
Find the equation of the line through the points A(–1, 3) and B(0, 2). Hence, show that the point A, B and C(1, 1) are collinear.
उत्तर
Slop of line AB = m = `(2 - 3)/(0 - 1(-1)) = (-1)/1 = -1`
Using the slope-point from, the equation of line AB is given by
y – y1 = m(x – x1)
i.e. y – 3 = –1[x – (–1)]
i.e. y – 3 = –1(x + 1)
i.e. y – 3 = –x – 1
i.e. x + y = 2
Now, slope of line BC = `(1 - 2)/(1 - 0) = -1/1 = -1`
Since, slope of line AB = slope of line BC.
Point A, B and C are collinear.
APPEARS IN
संबंधित प्रश्न
Write the equation of each of the following lines:
- The x-axis and the y-axis.
- The line passing through the origin and the point (-3, 5).
- The line passing through the point (-3, 4) and parallel to X-axis.
Find the slope and y-intercept of the line:
3x – 4y = 5
Is the line 3x + 4y + 7 = 0 perpendicular to the line 28x – 21y + 50 = 0?
Find the equation of the line passing through (−2, 1) and perpendicular to 4x + 5y = 6.
- Write down the equation of the line AB, through (3, 2) and perpendicular to the line 2y = 3x + 5.
- AB meets the x-axis at A and the y-axis at B. Write down the co-ordinates of A and B. Calculate the area of triangle OAB, where O is the origin.
Verify that points P(–2, 2), Q(2, 2) and R(2, 7) are vertices of a right angled triangle.
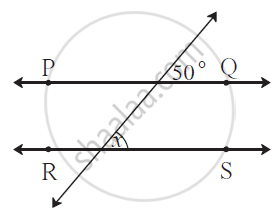
In the figure, line PQ || line RS. Using the information given
in the figure find the value of x.
Find:
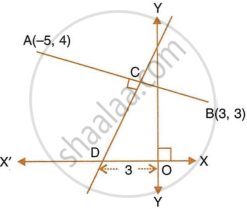
- equation of AB
- equation of CD
A straight line passes through the points P(–1, 4) and Q(5, –2). It intersects x-axis at point A and y-axis at point B. M is the mid-point of the line segment AB. Find:
- the equation of the line.
- the co-ordinates of point A and B.
- the co-ordinates of point M.
Three vertices of a parallelogram ABCD taken in order are A(3, 6), B(5, 10) and C(3, 2), find:
- the co-ordinates of the fourth vertex D.
- length of diagonal BD.
- equation of side AB of the parallelogram ABCD.
