Advertisements
Advertisements
प्रश्न
Prove that :
“If a line parallel to a side of a triangle intersects the remaining sides in two distince points, then the line divides the sides in the same proportion.”
उत्तर
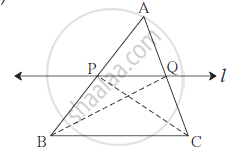
Given :In ΔABC line l || Side BC line l intersects side AB and side AC in P and Q respectively.
To prove : `(AP)/(PB) = (AQ)/(QC)`
Construction : Draw seg PC and seg QB.
Proof : `(A(APQ))/(A(PQB)) = (AP)/(PB)` ...... (I) (Areas are in proportion to the bases) `(A(APQ))/(A(PQB)) = (AQ)/(QC)` ....... (II) (Areas are in proportion to the bases) Δ PQB and Δ PQC have the same base PQ and PQ || BC,
their height is also same.
∴ A(Δ PQB) = A(Δ PQC) ..... (III)
∴` (A(APQ))/(A(PQB)) =( A(APQ))/(A(PQC))` ........ from ((I), (II) and (III)
∴ `(AP)/(PB) = (AQ)/(QC)` ........ from (I) , (II)
APPEARS IN
संबंधित प्रश्न
In ΔABC, A(3, 5), B(7, 8) and C(1, –10). Find the equation of the median through A.
Is the line x – 3y = 4 perpendicular to the line 3x – y = 7?
Is the line 3x + 2y = 5 parallel to the line x + 2y = 1?
Find the equation of the line passing through (−2, 1) and perpendicular to 4x + 5y = 6.
Find the equation of the perpendicular bisector of the line segment obtained on joining the points (6, −3) and (0, 3).
B(−5, 6) and D(1, 4) are the vertices of rhombus ABCD. Find the equations of diagonals BD and AC.
- Write down the equation of the line AB, through (3, 2) and perpendicular to the line 2y = 3x + 5.
- AB meets the x-axis at A and the y-axis at B. Write down the co-ordinates of A and B. Calculate the area of triangle OAB, where O is the origin.
The line 4x − 3y + 12 = 0 meets x-axis at A. Write the co-ordinates of A. Determine the equation of the line through A and perpendicular to 4x – 3y + 12 = 0.
The point P is the foot of perpendicular from A(−5, 7) to the line whose equation is 2x – 3y + 18 = 0. Determine :
- the equation of the line AP.
- the co-ordinates of P.
Find the point on the X–axis which is equidistant from A(–3, 4) and B(1, –4).
Verify that points P(–2, 2), Q(2, 2) and R(2, 7) are vertices of a right angled triangle.
A straight line passes through the points P(–1, 4) and Q(5, –2). It intersects x-axis at point A and y-axis at point B. M is the mid-point of the line segment AB. Find:
- the equation of the line.
- the co-ordinates of point A and B.
- the co-ordinates of point M.
In the given figure, line AB meets y-axis at point A. Line through C(2, 10) and D intersects line AB at right angle at point P. Find:
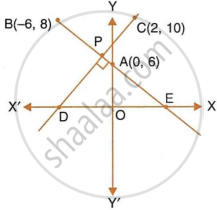
- equation of line AB.
- equation of line CD.
- co-ordinates of points E and D.
Find the equation of line through the intersection of lines 2x – y = 1 and 3x + 2y = –9 and making an angle of 30° with positive direction of x-axis.
Find the equation of the line through the points A(–1, 3) and B(0, 2). Hence, show that the point A, B and C(1, 1) are collinear.
Three vertices of a parallelogram ABCD taken in order are A(3, 6), B(5, 10) and C(3, 2), find:
- the co-ordinates of the fourth vertex D.
- length of diagonal BD.
- equation of side AB of the parallelogram ABCD.
In the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
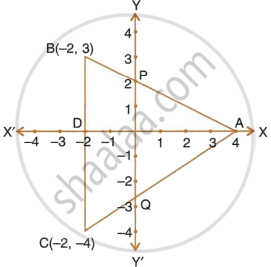
- Write the co-ordinates of A.
- Find the length of AB and AC.
- Find the radio in which Q divides AC.
- Find the equation of the line AC.
A line is parallel to Y-axis and is at a distance of 5 units from the Y-axis. Write the equation of that line.
A line segment joining P(2, –3) and Q(0, –1) is cut by the x-axis at the point R. A line AB cuts the y-axis at T(0, 6) and is perpendicular to PQ at S.
Find the:
- equation of line PQ
- equation of line AB
- coordinates of points R and S.
