Advertisements
Advertisements
प्रश्न
Prove that :
“If a line parallel to a side of a triangle intersects the remaining sides in two distince points, then the line divides the sides in the same proportion.”
उत्तर
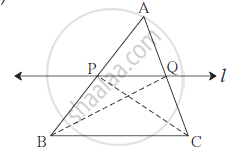
Given :In ΔABC line l || Side BC line l intersects side AB and side AC in P and Q respectively.
To prove : `(AP)/(PB) = (AQ)/(QC)`
Construction : Draw seg PC and seg QB.
Proof : `(A(APQ))/(A(PQB)) = (AP)/(PB)` ...... (I) (Areas are in proportion to the bases) `(A(APQ))/(A(PQB)) = (AQ)/(QC)` ....... (II) (Areas are in proportion to the bases) Δ PQB and Δ PQC have the same base PQ and PQ || BC,
their height is also same.
∴ A(Δ PQB) = A(Δ PQC) ..... (III)
∴` (A(APQ))/(A(PQB)) =( A(APQ))/(A(PQC))` ........ from ((I), (II) and (III)
∴ `(AP)/(PB) = (AQ)/(QC)` ........ from (I) , (II)
APPEARS IN
संबंधित प्रश्न
A (5, 4), B (-3, -2) and C (1, -8) are the vertices of a triangle ABC. Find the equations of the median AD and line parallel to AC passing through the point B.
Given 3x + 2y + 4 = 0
(i) express the equation in the form y = mx + c
(ii) Find the slope and y-intercept of the line 3x + 2y + 4 = 0
Find the slope and y-intercept of the line:
y = 4
The equation of a line is x – y = 4. Find its slope and y-intercept. Also, find its inclination.
Is the line 3x + 4y + 7 = 0 perpendicular to the line 28x – 21y + 50 = 0?
The line 4x − 3y + 12 = 0 meets x-axis at A. Write the co-ordinates of A. Determine the equation of the line through A and perpendicular to 4x – 3y + 12 = 0.
The point P is the foot of perpendicular from A(−5, 7) to the line whose equation is 2x – 3y + 18 = 0. Determine :
- the equation of the line AP.
- the co-ordinates of P.
A (5, 4), B (–3,–2) and C (1,–8) are the vertices of a triangle ABC. Find the equation of median AD and line parallel to AB passing through point C.
Show that points P(2, –2), Q(7, 3), R(11, –1) and S (6, –6) are vertices of a parallelogram.
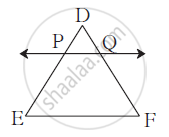
In Δ DEF, line PQ || side EF, If DP = 2.4,
PE = 7.2, DQ = 1 then find QF.
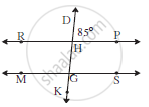
In the adjoining figure line RP ||line MS , line DK is a transversal . If ∠DHP = 85° find ∠RHG and ∠HGS.
Line PQ is parallel to line RS where points P,Q,R and S have
co-ordinates (2, 4), (3, 6), (3, 1) and (5, k) respectively. Find value of k.
In the given figure, line AB meets y-axis at point A. Line through C(2, 10) and D intersects line AB at right angle at point P. Find:
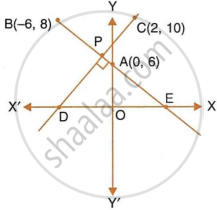
- equation of line AB.
- equation of line CD.
- co-ordinates of points E and D.
Find the equation of the line through the points A(–1, 3) and B(0, 2). Hence, show that the point A, B and C(1, 1) are collinear.
Find the equation of the line passing through the points (4,-5) and (-1,-2).
A line is parallel to Y-axis and is at a distance of 5 units from the Y-axis. Write the equation of that line.
