Advertisements
Advertisements
प्रश्न
Find the equation of the line passing through the points (4,-5) and (-1,-2).
उत्तर
Equation of line passing through points (x1,y1) and (x2,y2) is given by
`(x - x_1)/(x_1 - x_2) = (y - y_1)/(y_1 - y_2)`
Here (x1,y1) = (4,-5) and (x2,y2) = (-1,-2)
Equation of line passing through (4,-5) and (-1,-2) is given by
`(x - 4)/(4 - (-1)) = (y - (-5))/((-5) - (-2))`
∴ `(x - 4)/5 = (y + 5)/-3`
∴ (-3)(x-4) = 5(y + 5)
∴ - 3x + 12 = 5y + 25
∴ 12 – 25 = 5y + 3x
∴ 3x + 5y = - 13
∴ 3x + 5y + 13 = 0
Therefore equation of line passing through (4,-5) and (-1,-2) is 3x + 5y + 13 = 0
APPEARS IN
संबंधित प्रश्न
Write the equation of the line passing through the pair of points (2, 3) and (4, 7) in the form of y = mx + c.
If (4,-3) is a point on the line AB and slope of the line is (-2), write the equation of the line AB.
Find the slope and y-intercept of the line:
y = 4
Find the slope and y-intercept of the line:
3x – 4y = 5
Is the line 3x + 4y + 7 = 0 perpendicular to the line 28x – 21y + 50 = 0?
Is the line x – 3y = 4 perpendicular to the line 3x – y = 7?
A = (7, −2) and C = (−1, −6) are the vertices of square ABCD. Find the equations of diagonals AC and BD.
The point P is the foot of perpendicular from A(−5, 7) to the line whose equation is 2x – 3y + 18 = 0. Determine :
- the equation of the line AP.
- the co-ordinates of P.
The points A, B and C are (4, 0), (2, 2) and (0, 6) respectively. Find the equations of AB and BC. If AB cuts the y-axis at P and BC cuts the x-axis at Q, find the co-ordinates of P and Q.
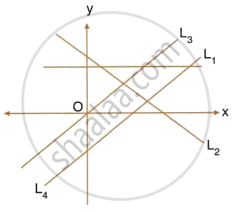
Match the equations A, B, C and D with the lines L1, L2, L3 and L4, whose graphs are roughly drawn in the given diagram.
A ≡ y = 2x;
B ≡ y – 2x + 2 = 0;
C ≡ 3x + 2y = 6;
D ≡ y = 2
Find the point on the X–axis which is equidistant from A(–3, 4) and B(1, –4).
Show that points P(2, –2), Q(7, 3), R(11, –1) and S (6, –6) are vertices of a parallelogram.
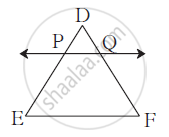
In Δ DEF, line PQ || side EF, If DP = 2.4,
PE = 7.2, DQ = 1 then find QF.
A line through point P(4, 3) meets x-axis at point A and the y-axis at point B. If BP is double of PA, find the equation of AB.
Find the equation of line through the intersection of lines 2x – y = 1 and 3x + 2y = –9 and making an angle of 30° with positive direction of x-axis.
In the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
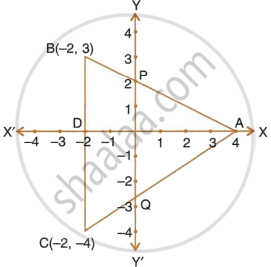
- Write the co-ordinates of A.
- Find the length of AB and AC.
- Find the radio in which Q divides AC.
- Find the equation of the line AC.
If (4,-3) is a point on line 5x +8y = c, find the value of c.
