Advertisements
Advertisements
प्रश्न
Prove that the lengths of two tangent segments drawn to the circle from an external point are equal.
उत्तर
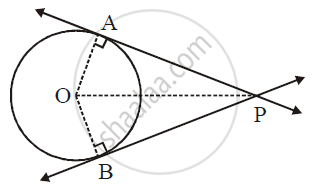
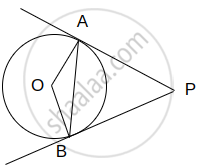
Given: O is the centre of the circle and P is a point in the exterior of the circle. A and B are the points of contact of the two tangents from P to the circle.
To Prove: PA = PB
Construction: Draw seg OA, seg OB, and seg OP.
Proof: Line AP ⊥ radius OA and line BP ⊥ radius OB ... (Tangent perpendicular to radius)
∴ `angle"PAO" = angle"PBO" = 90^@`
In right-angled triangles `triangle "OAP"` and `triangle"OBP"`
hypotenuse OP ≅ hypotenuse OP ...(Common side)
seg OA ≅ seg OB ...(Radii of the same circle)
`:.triangle"OAP" ≅ triangle"OBP"` ...(Hypotenuse-side of theorem)
∴ seg PA ≅ seg PB ...(c.s.c.t.)
∴ PA = PB
APPEARS IN
संबंधित प्रश्न
In the below given figure, two tangents RQ and RP are drawn from an external point R to the circle with centre O. If∠PRQ = 120°, then prove that OR = PR + RQ.

From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is ______.
The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
In the given figure, XY and X’Y’ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°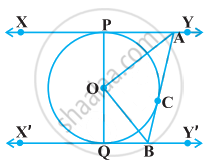
In the given figure PA = 10, PB = 2 and PC = 5. Find PD.
PQ is a tangent drawn from an external point P to a circle with centre O, QOR is the diameter of the circle. If ∠POR = 120°, what is the measure of ∠OPQ?
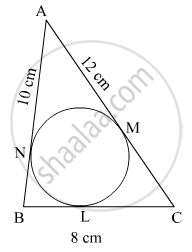
In Fig. 4, a circle is inscribed in a ΔABC having sides BC = 8 cm, AB = 10 cm and AC = 12 cm. Find the lengths BL, CM and AN.
Construct a pair of tangents to a circle of radius 4 cm from a point which is at a distance of 6 cm from its centre.
The length of the tangent from an external point P on a circle with centre O is ______
The length of the tangent from an external point on a circle is ______
In a circle of radius 5 cm, AB and AC are the two chords such that AB = AC = 6 cm. Find the length of the chord BC.
In a circle of radius 17 cm, two parallel chords are drawn on opposite sides of a diameter. The distance between the chords is 23 cm. If the length of one chord is 16 cm, then the length of the other is ______
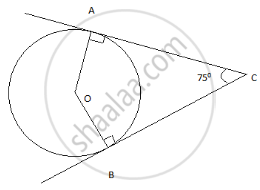
In fig, O is the centre of the circle, CA is tangent at A and CB is tangent at B drawn to the circle. If ∠ACB = 75°, then ∠AOB = ______
If from an external point B of a circle with centre O, two tangents BC and BD are drawn such that ∠DBC = 120°, prove that BC + BD = BO, i.e., BO = 2BC.
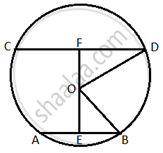
In figure, common tangents AB and CD to two circles intersect at E. Prove that AB = CD.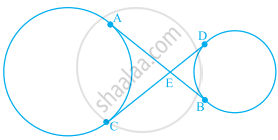
From an external point P, two tangents, PA and PB are drawn to a circle with centre O. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA = 10 cm, find the the perimeter of the triangle PCD.
Draw two concentric circles of radii 2 cm and 3 cm. From a point on the outer circle, construct a pair of tangents to the inner circle.
PA and PB are tangents drawn to the circle with centre O as shown in the figure. Prove that ∠APB = 2∠OAB.

PA and PB are tangents drawn to a circle of centre O from an external point P. Chord AB makes an angle of 30° with the radius at the point of contact. If length of the chord is 6 cm, find the length of the tangent PA and the length of the radius OA.