Advertisements
Advertisements
प्रश्न
A tree is broken by the wind. The top struck the ground at an angle of 30° and at a distance 30 m from the root. Find the whole height of the tree. (`sqrt(3)`=1.73)
उत्तर
Let AB represent the height of the tree.
Let the tree break at point C.
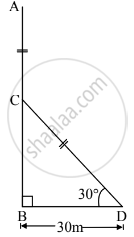
AC is the broken part of the which takes position CD such that ∠CDB = 30°
∴ Ac = CD ....(1)
In right-angled ΔCBD,
tan 30° = `(BC)/(BD)`
∴`1/sqrt(3) = (BC)/30`
∴ BC = `30/sqrt(3)`
cos 30° = `(BD)/(CD)`
∴ `sqrt(3)/2 = 30/(CD)`
∴ `sqrt(3) xx CD = 30 xx2 `
∴CD `60/sqrt3`
Ab = AC + BC .....[A-C-B]
∴ AB = CD + BC ... [From (i)]
∴ AB =`60/sqrt3 + 30/ sqrt 3`
∴ AB = `90/sqrt3 = 90/ sqrt3 xx sqrt3/ sqrt3` ....[Rationalizing the denominator]
∴ AB `(90sqrt3)/3 = 30sqrt3 = 30 xx 1.73 = 51.9` m
∴ Height of the tree is 51.9 m.
APPEARS IN
संबंधित प्रश्न
The angle of elevation of an aeroplane from a point on the ground is 60°. After a flight of 30 seconds the angle of elevation becomes 300 If the aeroplane is flying at a constant height of 3000 3 m, find the speed of the aeroplane.
Two ships are there in the sea on either side of a light house in such a way that the ships and the light house are in the same straight line. The angles of depression of two ships as observed from the top of the light house are 60° and 45°. If the height of the light house is 200 m, find the distance between the two ships. [use √3=1.73]
If a vertical pole 6m high has a shadow of length 2 √3 metres, find the angle of elevation of the sun.
The ratio of the height of a tower and the length of its shadow on the ground is `sqrt3 : 1`. What is the angle of elevation of the sun?
An observer finds the angle of elevation of the top of the tower from a certain point on the ground as 30°. If the observe moves 20 m towards the base of the tower, the angle of elevation of the top increases by 15°, find the height of the tower.
A tower stands vertically on the ground. From a point on the ground, 20 m away from the foot of the tower, the angle of elevation of the top of the tower is 600. What is the height of the tower?
The angle of elevation of the top of a tower from a point A on the ground is 30°. Moving a distance of 20metres towards the foot of the tower to a point B the angle of elevation increases to 60°. Find the height of the tower & the distance of the tower from the point A.
The horizontal distance between two poles is 15 m. The angle of depression of the top of first pole as seen from the top of second pole is 30°. If the height of the second pole is 24 m, find the height of the first pole. Use`[sqrt3=1.732]`
Two poles are 'a' metres apart and the height of one is double of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the smaller is
Find the angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of a tower of height `10sqrt(3)` m
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the difference between height of the lamp post and the apartment
A tower is 60 m heigh. Its shadow is x metres shorter when the sun’s altitude is 45° than when it has been 30°, then x is equal to
In figure given ABCD is a rectangle, the value of CE is ____________.

The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30°. The length of the tower is ____________.
A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 2m and is inclined at an angle of 30° to the ground. What should be the length of the slide?
A vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flagstaff are α and β, respectively. Then the height of the tower is ____________.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag staff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flag staff are α and β, respectively. Prove that the height of the tower is `((h tan α)/(tan β - tan α))`.
Let AB and PQ be two vertical poles, 160 m apart from each other. Let C be the middle point of B and Q, which are feet of these two poles. Let `π/8` and θ be the angles of elevation from C to P and A, respectively. If the height of pole PQ is twice the height of pole AB, then, tan2 θ is equal to ______.
