Advertisements
Advertisements
प्रश्न
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag staff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flag staff are α and β, respectively. Prove that the height of the tower is `((h tan α)/(tan β - tan α))`.
उत्तर
Given that a vertical flag staff of height h is surmounted on a vertical tower of height H(say), such that FP = h and FO = H.
The angle of elevation of the bottom and top of the flag staff on the plane is ∠PRO = α and ∠FRO = β respectively.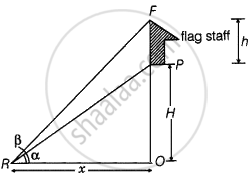
In ∆PRO, we have
tan α = `"PO"/"RO" = "H"/x` ...`[∵ tan θ = "Perpendicular"/"base"]`
⇒ x = `"H"/tan α` ...[Equation 1]
And in ∆FRO, we have
tan β = `"FO"/"RO" = ("FP" + "PO")/"RO"`
tan β = `("h" + "H")/x`
⇒ x = `("h" + "H")/tan β` ...[Equation 2]
Comparing equation 1 and equation 2,
⇒ `"H"/tan α = ("h" + "H")/tan β`
Solving for H,
⇒ H tan β = (h + H) tan α
⇒ H tan β – H tan α = h tan α
⇒ H (tan β – tan α) = h tan α
⇒ H = `("h" tan α)/(tan β - tan α)`
Hence, proved.
APPEARS IN
संबंधित प्रश्न
The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45°. If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60°, then find the height of the flagstaff. [use √3=1.73]
When the sun is 30º above the horizontal, Find the length of shadow cast by a building 50m high
An aeroplane when flying at a height of 4000m from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60º and 45º respectively. Find the vertical distance between the aeroplanes at that instant
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.

Two men on either side of a 75 m high building and in line with base of building observe the angles of elevation of the top of the building as 30° and 60°. Find the distance between the two men. (Use\[\sqrt{3} = 1 . 73\])
From the top of a light house, the angles of depression of two ships on the opposite sides of it are observed to be α and β. If the height of the light house be h metres and the line joining the ships passes through the foot of the light house, show that the distance between the ship is
`(h (tan ∝+tan ß))/ (tan ∝+tan ∝)`
The angle of elevation of the top of a cell phone tower from the foot of a high apartment is 60° and the angle of depression of the foot of the tower from the top of the apartment is 30°. If the height of the apartment is 50 m, find the height of the cell phone tower. According to radiation control norms, the minimum height of a cell phone tower should be 120 m. State if the height of the above mentioned cell phone tower meets the radiation norms
Two persons are standing ‘x’ metres apart from each other and the height of the first person is double that of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the shorter person (in metres) is
Two ships are sailing in the sea on either side of the lighthouse. The angles of depression of two ships as observed from the top of the lighthouse are 60° and 45° respectively. If the distance between the ships is `200[(sqrt(3) + 1)/sqrt(3)]` metres, find the height of the lighthouse.
The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Find the height of the tower.
