Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of a cell phone tower from the foot of a high apartment is 60° and the angle of depression of the foot of the tower from the top of the apartment is 30°. If the height of the apartment is 50 m, find the height of the cell phone tower. According to radiation control norms, the minimum height of a cell phone tower should be 120 m. State if the height of the above mentioned cell phone tower meets the radiation norms
उत्तर
Let the height of the cell phone tower be h m
AD is the height of the apartment; AD = 50 m
Let AB be x
In the right triangle ABC
tan 60° = `"BC"/"AB"`
`sqrt(3) = "h"/x`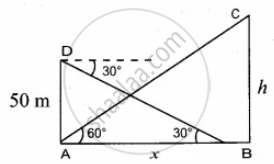
x = `"h"/sqrt(3)` ...(1)
In the right triangle ABD, tan 30° = `"AD"/"AB"`
`1/sqrt(3) = 50/x`
x = `50sqrt(3)` ...(2)
From (1) and (2) We get
`"h"/sqrt(3) = 50sqrt(3)`
h = `50sqrt(3) xx sqrt(3)`
= 50 × 3
= 150
Height of the cell phone tower is 150 m.
Yes, the cell phone tower meets the radiation norms.
APPEARS IN
संबंधित प्रश्न
A truck covers a distance of 150 km at a certain average speed and then covers another 200 km at an average speed which is 20 km per hour more than the first speed. If the truck covers the total distance in 5 hours, find the first speed of the truck.
A 21 m deep well with diameter 6 m is dug and the earth from digging is evenly spread to form a platform 27 m ✕ 11 m. Find the height of the platform.[Use `pi=22/7`]
PQ is a post of given height a, and AB is a tower at some distance. If α and β are the angles of elevation of B, the top of the tower, at P and Q respectively. Find the height of the tower and its distance from the post.
A statue 1.46m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the status is 60 and from the same point, the angle of elevation of the top of the pedestal is 45 . Find the height of the pedestal.
Two buildings are in front of each other on either side of a road of width 10 metres. From the top of the first building which is 20 metres high, the angle of elevation to the top of the second is 45°. What is the height of the second building?
On a morning walk, three persons step out together and their steps measure 30 cm, 36 cm, and 40 cm respectively. What is the minimum distance each should walk so that each can cover the same distance in complete steps?
Two poles are 25 m and 15 m high, and the line joining their tops makes an angle of 45° with the horizontal. The distance between these poles is ______.
The angles of depression of the top and the bottom of a 10 m tall building from the top of a multi-storeyed building are 30° and 45°, respectively. Find the height of the multi-storeyed building.
If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top ____________.
If the height of the tower is equal to the length of its shadow, then the angle of elevation of the sun is ______.
