Question

If the angle of elevation of a cloud from a point ‘h’ metres above a lake is θ₁ and the angle of depression of its reflection in the lake is θ₂. Prove that the height that the cloud is located from the ground is `("h"(tan theta_1  +  tan theta_2))/(tan theta_2  -  tan theta_1)`

Answer 1

Let P be the cloud and Q be its reflection.

Let A be the point of observation such that AB = h

Let the height of the cloud be x.  ...(PS = x)

PR = x – h and QR = x + h

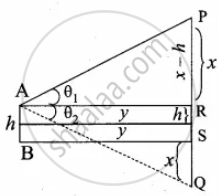
Let AR = y

In the right ∆ARP, tan θ₁ = `"PR"/"AR"`

tan θ₁ = `(x - "h")/y`   ...(1)

In the ∆AQR,

tan θ₂ = `"QR"/"AR"`

tan θ₂ = `(x + "h")/y`  ...(2)

Add (1) and (2)

tan θ₁ + tan θ₂ = `(x - "h")/y + (x + "h")/y`

= `(x - "h" + x + "h")/y`

= `(2x)/y`

Subtract (2) and (1)

tan θ₂ − tan θ₁ = `(x + "h")/y - (x - "h")/y`

= `(x + "h" - x + "h")/y`

= `(2"h")/y`

`((tan theta_1 + tan theta_2))/(tan theta_2 - tan theta_1) = (2x)/y ÷ (2"h")/y`

= `(2x)/y xx y/(2"h")`

= `x/"h"`

∴ x = `("h"(tan theta_1  +  tan theta_2))/(tan theta_2  -  tan theta_1)`

Hence the proof.