Advertisements
Advertisements
प्रश्न
If the angle of elevation of a cloud from a point ‘h’ metres above a lake is θ1 and the angle of depression of its reflection in the lake is θ2. Prove that the height that the cloud is located from the ground is `("h"(tan theta_1 + tan theta_2))/(tan theta_2 - tan theta_1)`
उत्तर
Let P be the cloud and Q be its reflection.
Let A be the point of observation such that AB = h
Let the height of the cloud be x. ...(PS = x)
PR = x – h and QR = x + h
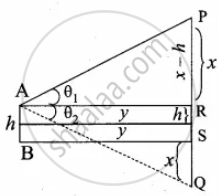
Let AR = y
In the right ∆ARP, tan θ1 = `"PR"/"AR"`
tan θ1 = `(x - "h")/y` ...(1)
In the ∆AQR,
tan θ2 = `"QR"/"AR"`
tan θ2 = `(x + "h")/y` ...(2)
Add (1) and (2)
tan θ1 + tan θ2 = `(x - "h")/y + (x + "h")/y`
= `(x - "h" + x + "h")/y`
= `(2x)/y`
Subtract (2) and (1)
tan θ2 − tan θ1 = `(x + "h")/y - (x - "h")/y`
= `(x + "h" - x + "h")/y`
= `(2"h")/y`
`((tan theta_1 + tan theta_2))/(tan theta_2 - tan theta_1) = (2x)/y ÷ (2"h")/y`
= `(2x)/y xx y/(2"h")`
= `x/"h"`
∴ x = `("h"(tan theta_1 + tan theta_2))/(tan theta_2 - tan theta_1)`
Hence the proof.
APPEARS IN
संबंधित प्रश्न
From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. Find the height of the tower
A fire in a building B is reported on the telephone to two fire stations P and Q, 20 km apart from each other on a straight road. P observes that the fire is at an angle of 60° to the road and Q observes that it is at an angle of 45° to the road. Which station should send its team and how much will this team have to travel?
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60° . At a point Y, 40m vertically above X, the angle of elevation is 45° . Find the height of tower PQ.
The radius (in cm) of the largest right circular cone that can be cut out from a cube of edge 4.2 cm is
A ladder on the platform of a fire brigade van can be elevated at an angle of 70° to the maximum. The length of the ladder can be extended upto 20 m. If the platform is 2m above the ground, find the maximum height from the ground upto which the ladder can reach. (sin 70° = 0.94)
If the angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower in the same straight line with it are complementary, find the height of the tower.
In the following figure, what are the angles of depression from the observing position O1 and O2of the object at A?
The angle of elevation of the top of a tower at a point on the ground 50 m away from the foot of the tower is 45º. Then the height of the tower (in metres) is
From the top of the tower 60 m high the angles of depression of the top and bottom of a vertical lamp post are observed to be 38° and 60° respectively. Find the height of the lamp post (tan 38° = 0.7813, `sqrt(3)` = 1.732)
The top of a banquet hall has an angle of elevation of 45° from the foot of a transmission tower and the angle of elevation of the topmost point of the tower from the foot of the banquet hall is 60°. If the tower is 60 m high, find the height of the banquet hall in decimals.
