Advertisements
Advertisements
प्रश्न
A fire in a building B is reported on the telephone to two fire stations P and Q, 20 km apart from each other on a straight road. P observes that the fire is at an angle of 60° to the road and Q observes that it is at an angle of 45° to the road. Which station should send its team and how much will this team have to travel?
उत्तर
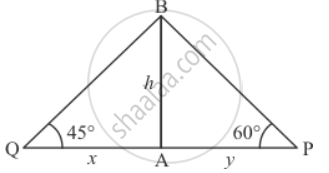
Let AB be the building of height h. P Observes that the fire is at an angle of 60° to the road and Q observes that the fire is at an angle of 45° to the road.
Let QA = x, AP = y. And `∠BPA = 60^@`,∠BQA = 45°, given PQ = 20.
Here clearly ∠APB > ∠AQB
=> ∠ABP < ∠ABQ
=> AP < AQ
So station P is near to the building. Hence station P must send its team
We sketch the following figure
So we use trigonometric ratios.
In ΔPAB
`tan P = (AB)/(AP)`
`=> tan 60^@ = h/y`
`=> h = sqrt3y`
Again in ΔQAB
`=> tan Q = (AB)/(QA)`
`=> tan 45^@ = h/x`
`=> 1 = h/x`
`=> x = h`
Now
x + y = 20
`=> h + y = 20` [∵ x = h]
`=> sqrt3y + y = 20` [∵ `h = sqrt3y`]
`=> y = 20/(sqrt3 + 1) = 10(sqrt3 - 1)`
Hence the team from station P wil have to travel `10(sqrt3 - 1)` km
APPEARS IN
संबंधित प्रश्न
The angle of elevation of an aeroplane from point A on the ground is 60˚. After flight of 15 seconds, the angle of elevation changes to 30˚. If the aeroplane is flying at a constant height of 1500√3 m, find the speed of the plane in km/hr.
A 1.6 m tall girl stands at a distance of 3.2 m from a lamp-post and casts a shadow of 4.8 m on the ground. Find the height of the lamp-post by using (i) trigonometric ratios (ii) property of similar triangles.
Two men on either side of the cliff 80 m high observe the angles of an elevation of the top of the cliff to be 30° and 60° respectively. Find the distance between the two men.
Two men are on opposite side of tower. They measure the angles of elevation of the top of the tower as 30 and 45 respectively. If the height of the tower is 50 meters, find the distance between the two men.
An electrician has to repair an electric fault on a pole of height 4 meters. He needs to reach a point 1 meter below the top of the pole to undertake the repair work. What should be the length of the ladder that he should use, which when inclined at an angle of 60° to the horizontal would enable him to reach the required position?
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 84 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
The top of a 15 m high tower makes an angle of elevation of 60° with the bottom of an electronic pole and angle of elevation of 30° with the top of the pole. What is the height of the electric pole?
A 1.5 m tall boy is standing at some distance from a 31.5 m tall building. If he walks ’d’ m towards the building the angle of elevation of the top of the building changes from 30° to 60°. Find the length d. (Take `sqrt3 = 1.73`)
The angles of elevation of the bottom and the top of a flag fixed at the top of a 25 m high building are 30° and 60° respectively from a point on the ground. Find the height of the flag.
|
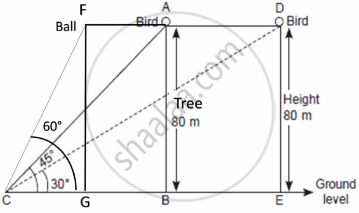
One evening, Kaushik was in a park. Children were playing cricket. Birds were singing on a nearby tree of height 80m. He observed a bird on the tree at an angle of elevation of 45°. When a sixer was hit, a ball flew through the tree frightening the bird to fly away. In 2 seconds, he observed the bird flying at the same height at an angle of elevation of 30° and the ball flying towards him at the same height at an angle of elevation of 60°.
|
- At what distance from the foot of the tree was he observing the bird sitting on the tree?
- How far did the bird fly in the mentioned time?
(or)
After hitting the tree, how far did the ball travel in the sky when Kaushik saw the ball? - What is the speed of the bird in m/min if it had flown `20(sqrt3 + 1) m`?