Advertisements
Advertisements
प्रश्न
A 1.6 m tall girl stands at a distance of 3.2 m from a lamp-post and casts a shadow of 4.8 m on the ground. Find the height of the lamp-post by using (i) trigonometric ratios (ii) property of similar triangles.
उत्तर
Let AC be the lamp post of height h
We assume that ED = 1.6 m, BE = 4.8 m and EC = 3.2 m
We have to find the height of the lamp post
Now we have to find the height of lamp post using similar triangles.
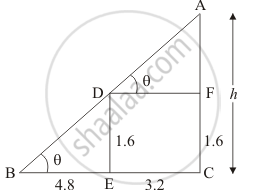
Since triangle BDE and triangle ABC are similar.
`(AC)/(BC) = (ED)/(BE)`
`h/(4.8 + 3.2) = 1.6/(BE)`
`h = 8/3`
Again, we have to find height of lamp post using trigonometric ratios.
In ΔADE
`=> tan theta = 1.6/4.8`
`=> tan theta = 1/3`
Again in ΔABC
`=> tan theta = h/(4.8 + 3.2)`
`=> 1/2 = h/8`
`h = 8/3`
Hence the height of lamp post is 8/3 m
APPEARS IN
संबंधित प्रश्न
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
On a straight line passing through the foot of a tower, two points C and D are at distances of 4 m and 16 m from the foot respectively. If the angles of elevation from C and D of the top of the tower are complementary, then find the height of the tower.
An aeroplane flying horizontally 1 km above the ground is observed at an elevation of 60°. After 10 seconds, its elevation is observed to be 30°. Find the speed of the aeroplane in km/hr.
A ladder 15 m long makes an angle of 60° with the wall. Find the height of the point where the ladder touches the wall.
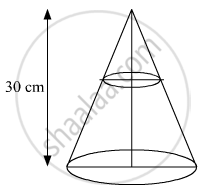
In fig. 9 is shown a right circular cone of height 30 cm. A small cone is cut off from the top by a plane parallel to the base. If the volume of the small cone is 127127 of the volume of cone, find at what height above the base is the section made.
The tops of two towers of height x and y, standing on level ground, subtend angles of 30º and 60º respectively at the centre of the line joining their feet, then find x : y.
From a light house the angles of depression of two ships on opposite sides of the light house are observed to be 30° and 45°. If the height of the light house is h metres, the distance between the ships is
A tower is 60 m heigh. Its shadow is x metres shorter when the sun’s altitude is 45° than when it has been 30°, then x is equal to
An observer 1.5 metres tall is 20.5 metres away from a tower 22 metres high. Determine the angle of elevation of the top of the tower from the eye of the observer.
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60°, then the distance between the two towers is ____________.
