Advertisements
Advertisements
प्रश्न
A tower is 60 m heigh. Its shadow is x metres shorter when the sun’s altitude is 45° than when it has been 30°, then x is equal to
पर्याय
41.92 m
43.92 m
43 m
45.6 m
उत्तर
43.92 m
Explanation;
Hint:
In the right ∆ABC, tan 30° = `"AB"/"BC" = 60/(x + y)`
`1/sqrt(3) = 60/(x + y)`
⇒ x + y = `60sqrt(3)`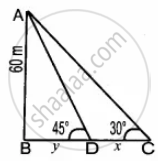
y = `60sqrt(3) - x` ...(1)
In the right ∆ABD, tan 45° = `"AB"/"BD"`
1 = `60/y`
⇒ y = 60 ...(2)
From (1) and (2) we get
60 = `60sqrt(3) - x`
x = `60 sqrt(3) - 60`
= `60(sqrt(3) - 1)`
= 60(1.732 – 1)
= 60 × 0.732
x = 43.92 m
APPEARS IN
संबंधित प्रश्न
The angle of elevation of an aeroplane from point A on the ground is 60˚. After flight of 15 seconds, the angle of elevation changes to 30˚. If the aeroplane is flying at a constant height of 1500√3 m, find the speed of the plane in km/hr.
At a point A, 20 metres above the level of water in a lake, the angle of elevation of a cloud is 30˚. The angle of depression of the reflection of the cloud in the lake, at A is 60˚.
Find the distance of the cloud from A.
The angles of depression of the top and bottom of a 50 m high building from the top of a tower are 45° and 60° respectively. Find the height of the tower and the horizontal distance between the tower and the building (use `sqrt3`=1.73)
A vessel full of water is in the form of an inverted cone of height 8 cm and the radius of its top, which is open, is 5 cm. 100 spherical lead balls are dropped into the vessel. One-fourth of the water flows out of the vessel. Find the radius of a spherical ball ?
The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of depression from the top of the tower to the foot of the hill is 30°. If the tower is 50 m high, find the height of the hill ?
What is the angle of elevation of the Sun when the length of the shadow of a vetical pole is equal to its height?
The ratio of the length of a rod and its shadow is `1 : sqrt3`. The angle of elevation of the sum is
The angle of elevation of the top of a tower at a point on the ground 50 m away from the foot of the tower is 45º. Then the height of the tower (in metres) is
The angles of depression of the top and the bottom of a 10 m tall building from the top of a multi-storeyed building are 30° and 45°, respectively. Find the height of the multi-storeyed building.
|
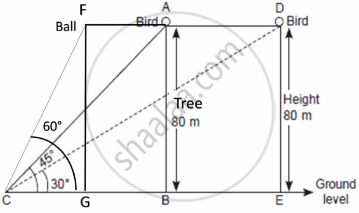
One evening, Kaushik was in a park. Children were playing cricket. Birds were singing on a nearby tree of height 80m. He observed a bird on the tree at an angle of elevation of 45°. When a sixer was hit, a ball flew through the tree frightening the bird to fly away. In 2 seconds, he observed the bird flying at the same height at an angle of elevation of 30° and the ball flying towards him at the same height at an angle of elevation of 60°.
|
- At what distance from the foot of the tree was he observing the bird sitting on the tree?
- How far did the bird fly in the mentioned time?
(or)
After hitting the tree, how far did the ball travel in the sky when Kaushik saw the ball? - What is the speed of the bird in m/min if it had flown `20(sqrt3 + 1) m`?