Advertisements
Advertisements
Question
A tower is 60 m heigh. Its shadow is x metres shorter when the sun’s altitude is 45° than when it has been 30°, then x is equal to
Options
41.92 m
43.92 m
43 m
45.6 m
Solution
43.92 m
Explanation;
Hint:
In the right ∆ABC, tan 30° = `"AB"/"BC" = 60/(x + y)`
`1/sqrt(3) = 60/(x + y)`
⇒ x + y = `60sqrt(3)`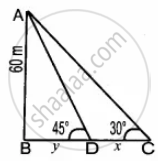
y = `60sqrt(3) - x` ...(1)
In the right ∆ABD, tan 45° = `"AB"/"BD"`
1 = `60/y`
⇒ y = 60 ...(2)
From (1) and (2) we get
60 = `60sqrt(3) - x`
x = `60 sqrt(3) - 60`
= `60(sqrt(3) - 1)`
= 60(1.732 – 1)
= 60 × 0.732
x = 43.92 m
APPEARS IN
RELATED QUESTIONS
A truck covers a distance of 150 km at a certain average speed and then covers another 200 km at an average speed which is 20 km per hour more than the first speed. If the truck covers the total distance in 5 hours, find the first speed of the truck.
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.

A moving boat is observed from the top of a 150 m high cliff moving away from the cliff. The angle of depression of the boat changes from 60° to 45° in 2 minutes. Find the speed of the boat in m/h.
The length of the shadow of a tower standing on the level plane is found to 2x meter longer when the sun's altitude is 30° than when it was 45°. Prove that the height of the tower is `x(sqrt3 + 1)` meters.
A man on the deck of a ship, 16m above water level, observe that that angle of elevation and depression respectively of the top and bottom of a cliff are 60° and 30° . Calculate the distance of the cliff from the ship and height of the cliff.
An observer, 1.7 m tall, is 203–√203 m away from a tower. The angle of elevation from the of observer to the top of tower is 30°. Find the height of tower ?
Find the angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of a tower of height `10sqrt(3)` m
The angles of depression of two objects from the top of a 100 m hill lying to its east are found to be 45° and 30°. Find the distance between the two objects. (Take `sqrt3 = 1.73`)
The shadow of a tower standing on a level plane is found to be 50 m longer when Sun’s elevation is 30° than when it is 60°. Then the height of the tower is ____________.
The angle of elevation of the top of a vertical tower from a point A, due east of it is 45°. The angle of elevation of the top of the same tower from a point B, due south of A is 30°. If the distance between A and B is `54sqrt(2)` m, then the height of the tower (in metres), is ______.
