Advertisements
Advertisements
Question
The length of the shadow of a tower standing on the level plane is found to 2x meter longer when the sun's altitude is 30° than when it was 45°. Prove that the height of the tower is `x(sqrt3 + 1)` meters.
Solution
Let AB be the tower of height hm. the length of the shadow of the tower to be found 2xmeters at the plane longer when sun’s altitude is 30° than when it was 45°.
Let BC = ym,
CD = 2x m and ∠ADB = 30°, ∠ACB = 45°
We have to find the height of the tower
`We have the corresponding figure as follows
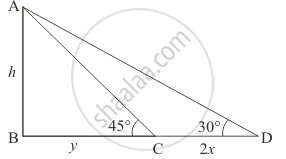
So we use trigonometric ratios.
In a triangle ABC
`=> tan C = (AB)/(BC)`
`=> tan 45^@ = h/y`
`=> 1 = h/y`
`=> y = h`
Again in a triangle ADB
`=> tan D = (AB)/(BC)`
`=> tan 45^@ = h/y`
`=> tan 30^@ = h/(2x + y)`
`=> 1/sqrt3 = h/(2x + y)`
`=> sqrt3h = 2x + y`
`=> h(sqrt3 - 1) = 2x`
`=> h = (2x)/(sqrt3 - 1)`
`=> h = x(sqrt3 + `)`
Hence the height of tower is `x(sqrt3 + 1)` m
APPEARS IN
RELATED QUESTIONS
Two building are in front of each other on either side of a road of width 10 metres. From the top of the first building which is 40 metres high, the angle of elevation to the top of the second is 45°. What is the height of the second building?
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are 60° and 30° respectively. Find the height of the tower.
A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the canal.

The length of a string between a kite and a point on the ground is 90 meters. If the string makes an angle O with the ground level such that tan O = 15/8, how high is the kite? Assume that there is no slack in the string.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flag-staff of height 5 meters. At a point on the plane, the angles of elevation of the bottom and the top of the flag-staff are respectively 300 and 600. Find the height of the tower.
If the height of a vertical pole is 3–√3 times the length of its shadow on the ground, then the angle of elevation of the Sun at that time is
(A) 30°
(B) 60°
(C) 45°
(D) 75°
A kite is flying at a height of 60 m above the ground. The string attached to the kite is tied at the ground. It makes an angle of 60° with the ground. Assuming that the string is straight, find the length of the string.
Find the distance between the points (a, b) and (−a, −b).
We all have seen the airplanes flying in the sky but might have not thought of how they actually reach the correct destination. Air Traffic Control (ATC) is a service provided by ground-based air traffic controllers who direct aircraft on the ground and through a given section of controlled airspace, and can provide advisory services to aircraft in non-controlled airspace. Actually, all this air traffic is managed and regulated by using various concepts based on coordinate geometry and trigonometry.
At a given instance, ATC finds that the angle of elevation of an airplane from a point on the ground is 60°. After a flight of 30 seconds, it is observed that the angle of elevation changes to 30°. The height of the plane remains constantly as `3000sqrt(3)` m. Use the above information to answer the questions that follow-
- Draw a neat labelled figure to show the above situation diagrammatically.
- What is the distance travelled by the plane in 30 seconds?
OR
Keeping the height constant, during the above flight, it was observed that after `15(sqrt(3) - 1)` seconds, the angle of elevation changed to 45°. How much is the distance travelled in that duration. - What is the speed of the plane in km/hr.
The angle of elevation of the top of a 15 m high tower at a point `15sqrt(3)` m away from the base of the tower is ______.
