Advertisements
Advertisements
प्रश्न
The length of the shadow of a tower standing on the level plane is found to 2x meter longer when the sun's altitude is 30° than when it was 45°. Prove that the height of the tower is `x(sqrt3 + 1)` meters.
उत्तर
Let AB be the tower of height hm. the length of the shadow of the tower to be found 2xmeters at the plane longer when sun’s altitude is 30° than when it was 45°.
Let BC = ym,
CD = 2x m and ∠ADB = 30°, ∠ACB = 45°
We have to find the height of the tower
`We have the corresponding figure as follows
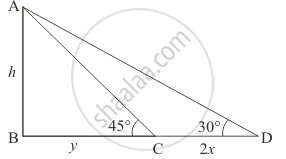
So we use trigonometric ratios.
In a triangle ABC
`=> tan C = (AB)/(BC)`
`=> tan 45^@ = h/y`
`=> 1 = h/y`
`=> y = h`
Again in a triangle ADB
`=> tan D = (AB)/(BC)`
`=> tan 45^@ = h/y`
`=> tan 30^@ = h/(2x + y)`
`=> 1/sqrt3 = h/(2x + y)`
`=> sqrt3h = 2x + y`
`=> h(sqrt3 - 1) = 2x`
`=> h = (2x)/(sqrt3 - 1)`
`=> h = x(sqrt3 + `)`
Hence the height of tower is `x(sqrt3 + 1)` m
APPEARS IN
संबंधित प्रश्न
The altitude of the sun at any instant is 60º. Find the height of the vertical pole that will cast a shadow of 30 m.
A statue, 1.6 m tall, stands on a top of pedestal, from a point on the ground, the angle of elevation of the top of statue is 60° and from the same point the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
A tower stands vertically on the ground. From a point on the ground, 20 m away from the foot of the tower, the angle of elevation of the top of the tower is 600. What is the height of the tower?
A tree is broken by the wind. The top struck the ground at an angle of 30° and at a distance 30 m from the root. Find the whole height of the tree. (`sqrt(3)`=1.73)
A road is flanked on either side by continuous rows of houses of height `4sqrt(3)` m with no space in between them. A pedestrian is standing on the median of the road facing a row house. The angle of elevation from the pedestrian to the top of the house is 30°. Find the width of the road
When the length of shadow of a vertical pole is equal to `sqrt3` times its height, the angle of elevation of the Sun’s altitude is ____________.
The upper part of a tree is broken by the wind and makes an angle of 30° with the ground. The distance from the foot of the tree to the point where the top touches the ground is 5 m. The height of the tree is ____________.
A tower stands vertically on the ground. From a point on the ground, which is 30 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 30°. Find the height of the tower.
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun is also increasing.
