Question

A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 7m. At a point on the plane, the angle of elevation of the bottom of the flagstaff is 30º and that of the top of the flagstaff is 45º. Find the height of the tower.

Answer 1

Let AB be the tower and BC be the flagstaff.

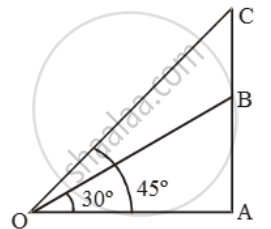
Then, BC = 7 m. Let AB = h.

Let O be the point of observation.

Then, ∠AOB = 30º and ∠AOC = 45º.

`\text{Now, }\frac{OA}{AC}=\text{cot 45}^\text{o}=1`

⇒ OA = AC = h + 7.

`\text{And, }\frac{OA}{AB}=\text{cot }30^\text{o}=\sqrt{3}`

`\Rightarrow \frac{OA}{h}=\sqrt{3}\Rightarrow OA=h\sqrt{3}`

∴ h + 7 = h√3

`\Rightarrow \frac{7}{\sqrt{3}-1}\times\frac{\sqrt{3}+1}{\sqrt{3}+1}=\frac{7(\sqrt{3}+1)}{2}=9.562\m`

Answer 2

Let BC be the tower of height hm. AB be the flagstaff of height 7 m on the tower and Dbe the point on the plane making an angle of elevation of the top of the flagstaff is 45° and angle of elevation of the bottom of the flagstaff is 30°.

Let CD = x, AB = 7 and ∠BDC = 30° and ∠ADC = 45°.

We to find the height of the tower

We have the corresponding figure as follows

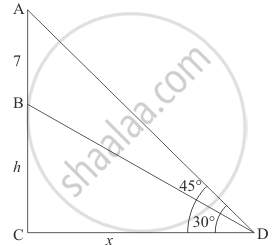
So we use trigonometric ratios.

In a triangle BCD

`=> tan D = (BC)/(CD)`

`=> tan 30^@ = h/x`

`=> 1/sqrt3 = h/x`

`=> x = sqrt3h`

Again in a triangle ADC

`=> tan D = (AB + BC)/(CD)`

`=> tan 45^@ = (h + 7)/x`

`=> 1 = (h + 7)/x`

`=> x = h + 7`

`=> sqrt3h = h + 7`

`=> h(sqrt3  - 1) = 7`

`=> h = 7/(sqrt3  - 1)`

`=> h = 9.56`

Hence the height of toweris 9.56 m