Advertisements
Advertisements
प्रश्न
An electrician has to repair an electric fault on a pole of height 4 meters. He needs to reach a point 1 meter below the top of the pole to undertake the repair work. What should be the length of the ladder that he should use, which when inclined at an angle of 60° to the horizontal would enable him to reach the required position?
उत्तर
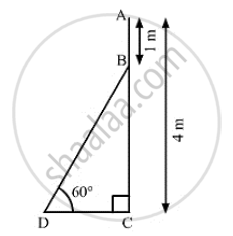
Let AC be the pole and BD be the ladder
We have,
AC = 4m, AB = 1m and ∠BDC = 60°
And, BC = AC - AB = 4-1= 3m
In ΔBDC,
`sin 60° = (BC)/(BD)`
`⇒sqrt(3)/2 =3/(BD)`
`⇒ BD = (3xx2)/sqrt(3)`
`⇒ BD = 2 sqrt(3)`
`⇒ BD = 2 xx 1.73`
∴ BD = 3.46 m
So, he should use 3.46 m long ladder to reach the required position.
APPEARS IN
संबंधित प्रश्न
The tops of two towers of height x and y, standing on level ground, subtend angles of 30° and 60° respectively at the centre of the line joining their feet, then find x, y.
From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. Find the height of the tower
A ladder rests against a wall at an angle α to the horizontal. Its foot is pulled away from the wall through a distance a so that it slides a distance b down the wall making an angle β with the horizontal. Show that `a/b = (cos alpha - cos beta)/(sin beta - sin alpha)`
An observer, 1.5 m tall, is 28.5 m away from a tower 30 m high. Determine the angle of elevation of the top of the tower from his eye.
From the top of a lighthouse, the angles of depression of two ships on the opposite sides of it are observed to be a and 3. If the height of the lighthouse be h meters and the line joining the ships passes through the foot of the lighthouse, show that the distance
`(h(tan alpha + tan beta))/(tan alpha tan beta)` meters
The angle of elevation of a cloud from a point h metre above a lake is θ. The angle of depression of its reflection in the lake is 45°. The height of the cloud is
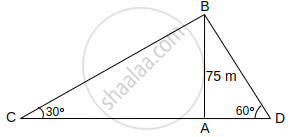
Two men on either side of a cliff 75 m high observe the angles of elevation of the top of the cliff to be 30° and 60°. Find the distance between the two men.
Two vertical poles AB = 15 m and CD = 10 m are standing apart on a horizontal ground with points A and C on the ground. If P is the point of intersection of BC and AD, then the height of P (in m) above the line AC is ______.
The angle of elevation of the top of a vertical tower from a point A, due east of it is 45°. The angle of elevation of the top of the same tower from a point B, due south of A is 30°. If the distance between A and B is `54sqrt(2)` m, then the height of the tower (in metres), is ______.
Two circles of radii 5 cm and 3 cm touch each other externally. Find the distance between their centres.
