Advertisements
Advertisements
प्रश्न
From the top of a vertical tower, the angles depression of two cars in the same straight line with the base of the tower, at an instant are found to be 45° and 60° . If the cars are 100 m apart and are on the same side of the tower, find the height of the tower.
उत्तर
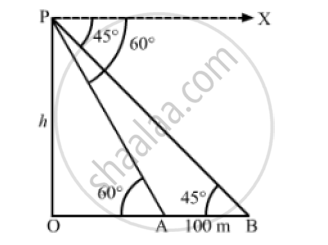
Let OP be the tower and points A and B be the positions of the cars.
We have,
AB =100m, ∠OAP = 60° and ∠OBP = 45°
Let OP = h
In ΔAOP,
` tan 60° = (OP)/(OA)`
`⇒ sqrt(3) = h/(OA)`
`⇒OA = h/sqrt(3)`
Also, in Δ BOP ,
` tan 45° = (OP)/(OB)`
`⇒ 1 = h/(OB)`
⇒ OB = h
Now,OB - OA = 100
`⇒ h - h/sqrt(3) = 100`
` ⇒ (h sqrt(3)-h)/sqrt(3) = 100`
`⇒(h(sqrt(3) -h))/sqrt(3) = 100`
`h = (100sqrt(3) )/((sqrt(3)-1)) xx ((sqrt(3)+1))/((sqrt(3)+1))`
`h = (100 sqrt(3) ( sqrt(3)+1))/((3-1))`
`⇒ h = (100(3+sqrt(3)))/2`
⇒ h = 50(3+1.732)
⇒ h =50(4.732)
∴ h =236.6m
So, the height of the tower is 236.6 m.
Disclaimer. The answer given in the textbook is incorrect. The same has been rectified above.
संबंधित प्रश्न
The horizontal distance between two trees of different heights is 60 m. The angle of depression of the top of the first tree, when seen from the top of the second tree, is 45°. If the height of the second tree is 80 m, find the height of the first tree.
A boy is standing on the ground and flying a kite with 100 m of string at an elevation of 30°. Another boy is sanding on the roof of a 10 m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
The angle of elevation of the top of a vertical tower from a point on the ground is 60° . From another point 10 m vertically above the first, its angle of elevation is 30° .Find the height of the tower.
The Distance of the point (−3, 4) from the x-axis is
It is found that on walking x meters towards a chimney in a horizontal line through its base, the elevation of its top changes from 30° to 60°. The height of the chimney is
A ladder makes an angle of 60º with the ground when placed against a wall. If the foot of the ladder is 2 m away from the wall, then the length of the ladder (in metres) is
On a morning walk, three persons step out together and their steps measure 30 cm, 36 cm, and 40 cm respectively. What is the minimum distance each should walk so that each can cover the same distance in complete steps?
The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point, 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.
As observed from the top of a light house 100 m above sea level, the angle of depression of a ship, sailing directly towards it, changes from 30° to 45°. Determine the distance travelled by the ship during this time. [Use `sqrt(3)` = 1.732]

Two vertical poles are 150 m apart and the height of one is three times that of the other. If from the middle point of the line joining their feet, an observer finds the angles of elevation of their tops to be complementary, then the height of the shorter pole (in meters) is ______.
