Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of a vertical tower from a point on the ground is 60° . From another point 10 m vertically above the first, its angle of elevation is 30° .Find the height of the tower.
उत्तर
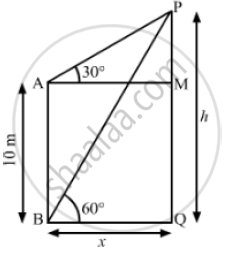
Let PQ be the tower
We have,
AB =10m,MAP = 30° and ∠PBQ = 60°
Also, MQ = AB =10m
Let BQ = x and PQ = h
So, AM = BQ = x and PM = PQ - MQ = h -10
In ΔBPQ,
` tan 60° = (PQ)/(BQ)`
`⇒ sqrt(3) = h/x`
`⇒ x = h/sqrt(3) ` ..............(1)
Now , in Δ AMP
` tan 30° = (PM) /( AM)`
`⇒ 1/ sqrt(3) = (h-10) /x`
`⇒h sqrt(3)-10 sqrt(3)=x`
`⇒ h sqrt(3) - 10 sqrt(3) = h/ sqrt(3) ` [ Using (1)]
⇒ 3h - 30=h
⇒ 3h - h = 30
⇒ 2h = 30
`⇒ h 30/2 `
∴ h = 15 m
So, the height of the tower is 15 m.
संबंधित प्रश्न
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 45°. If the tower is 30 m high, find the height of the building.
The angle of elevation of a cliff from a fixed point is θ. After going up a distance of k metres towards the top of cliff at an angle of φ, it is found that the angle of elevation is α. Show that the height of the cliff is metres
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground, making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
A tower stands vertically on the ground. From a point on the ground 20 m away from the foot of the tower, the angle of elevation of the top of the tower is 60°. What is the height of the tower?
In the following figure, what are the angles of depression from the observing position O1 and O2of the object at A?
The angles of depression of two ships from the top of a light house are 45° and 30° towards east. If the ships are 100 m apart. the height of the light house is
A man in a boat rowing away from a lighthouse 100 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 30°.
Find the speed of the boat in metres per minute. [Use `sqrt(3` = 1.732]Use 3=1.732">
The angles of depression of the top and the bottom of a 10 m tall building from the top of a multi-storeyed building are 30° and 45°, respectively. Find the height of the multi-storeyed building.
The top of a banquet hall has an angle of elevation of 45° from the foot of a transmission tower and the angle of elevation of the topmost point of the tower from the foot of the banquet hall is 60°. If the tower is 60 m high, find the height of the banquet hall in decimals.
Two pillars of equal lengths stand on either side of a road which is 100 m wide, exactly opposite to each other. At a point on the road between the pillars, the angles of elevation of the tops of the pillars are 60° and 30°. Find the length of each pillar and the distance of the point on the road from the pillars. (Use `sqrt3` = 1.732)
