Advertisements
Advertisements
प्रश्न
The top of a banquet hall has an angle of elevation of 45° from the foot of a transmission tower and the angle of elevation of the topmost point of the tower from the foot of the banquet hall is 60°. If the tower is 60 m high, find the height of the banquet hall in decimals.
उत्तर
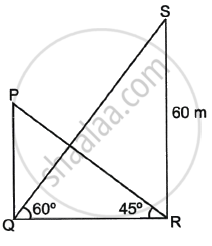
In the diagram, PQ represents the banquet hall and SR represents the transmission tower.
So, SR = 60 m, ∠SQR = 60° and ∠PRQ = 45°.
Now, in ΔSQR,
tan 60° = `(SR)/(QR)`
⇒ `sqrt(3) = 60/(QR)`
⇒ QR = `60/sqrt(3)`
= 34.64
Also, in ΔPQR,
tan 45° = `(PQ)/(QR)`
⇒ 1 = `(PQ)/(34.64)`
⇒ PQ = 34.64
As a result, the banquet hall's height is 34.64 m.
APPEARS IN
संबंधित प्रश्न
The angle of depression of a car parked on the road from the top of a 150 m high tower is 30°. The distance of the car from the tower (in metres) is
`(A) 50sqrt3`
`(B) 150sqrt 3`
`(C) 150sqrt2`
`(D) 75`
The altitude of the sun at any instant is 60º. Find the height of the vertical pole that will cast a shadow of 30 m.
When the sun is 30º above the horizontal, Find the length of shadow cast by a building 50m high
At the foot of a mountain the elevation of its summit is 45º; after ascending 1000 m towards the mountain up a slope of 30º inclination is found to be 60º. Find the height of the mountain.
An electric pole is 10 m high. A steel wire tied to the top of the pole is affixed at a point on the ground to keep the pole upright. If the wire makes an angle of 45° with the horizontal through the foot of the pole, find the length of the wire.
The angle of elevation of the top of a chimney form the foot of a tower is 60° and the angle of depression of the foot of the chimney from the top of the tower is 30° . If the height of the tower is 40 meters. Find the height of the chimney.
A man on the deck of a ship, 16m above water level, observe that that angle of elevation and depression respectively of the top and bottom of a cliff are 60° and 30° . Calculate the distance of the cliff from the ship and height of the cliff.
In Fig. 3, the area of triangle ABC (in sq. units) is:
Two buildings are facing each other on a road of width 12 metre. From the top of the first building, which is 10 metre high, the angle of elevation of the top of the second is found to be 60°. What is the height of the second building ?
Two poles of heights 18 metre and 7 metre are erected on a ground. The length of the wire fastened at their tops in 22 metre. Find the angle made by the wire with the horizontal.
When an observer at a distance of 12 m from a tree looks at the top of the tree, the angle of elevation is 60°. What is the height of the tree? `(sqrt 3 = 1.73)`
Find the positive value of m for which the distance between the points A(5, −3) and B(13, m) is 10 units.
A road is flanked on either side by continuous rows of houses of height `4sqrt(3)` m with no space in between them. A pedestrian is standing on the median of the road facing a row house. The angle of elevation from the pedestrian to the top of the house is 30°. Find the width of the road
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is B to the North of A?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
If at some time, the length of the shadow of a tower is `sqrt3` times its height, then the angle of elevation of the sun, at that time is ____________.
In given figure, the value of ZC is ____________.
In figure given ABCD is a rectangle, the value of CE is ____________.

A plane is observed to be approaching the airport. It is at a distance of 12 km from the point of observation and makes an angle of elevation of 60°. The height above the ground of the plane is ____________.
A ladder 15 meters long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then the height of the wall will be ____________.
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 3 m from the banks, find the width of the river. (Use `sqrt(3)` = 1.73)
