Advertisements
Advertisements
प्रश्न
The angle of elevation of the top of a chimney form the foot of a tower is 60° and the angle of depression of the foot of the chimney from the top of the tower is 30° . If the height of the tower is 40 meters. Find the height of the chimney.
The angle of elevation of the top of a chimney from the foot of a tower is 60° and the angle of depression of the foot of the chimney from the top of the tower is 30°. If the height of the tower is 40 m, find the height of the chimney. According to pollution control norms, the minimum height of a smoke emitting chimney should be 100 m. State if the height of the above mentioned chimney meets the pollution norms. What value is discussed in this question?
उत्तर
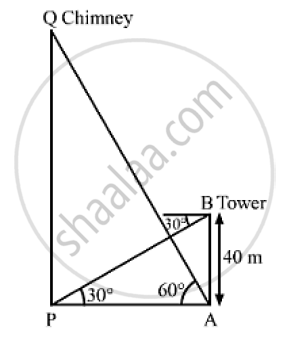
Let PQ be the chimney and AB be the tower.
We have,
AB = 40m,∠APB = 30° and ∠PAQ = 60°
In ΔABP,
`tan 30° = (AB)/(AP)`
`⇒ 1/ sqrt(3) = 40/ (AP)`
`⇒ AP = 40 sqrt(3 ) m`
Now, in Δ APQ ,
` tan 60° = (OQ)/(AP)`
`⇒ sqrt(3) = (PQ) / (40 sqrt(3))`
∴ PQ = 120 m
So, the height of the chimney is 120 m.
Hence, the height of the chimney meets the pollution norms.
In this question, management of air pollution has been shown
संबंधित प्रश्न
The angles of depression of the top and bottom of a 50 m high building from the top of a tower are 45° and 60° respectively. Find the height of the tower and the horizontal distance between the tower and the building (use `sqrt3`=1.73)
There is a small island in the middle of a 100 m wide river and a tall tree stands on the island. P and Q are points directly opposite to each other on two banks, and in line with the tree. If the angles of elevation of the top of the tree from P and Q are respectively 30º and 45º, find the height of the tree. (Use `sqrt(3)` = 1.732)
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m. from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
A man sitting at a height of 20 m on a tall tree on a small island in the middle of a river observes two poles directly opposite to each other on the two banks of the river and in line with the foot of the tree. If the angles of depression of the feet of the poles from a point at which the man is sitting on the tree on either side of the river are 60° and 30°respectively. Find the width of the river.
If the angle of elevation of a cloud from a point h meters above a lake is a and the angle of depression of its reflection in the lake be b, prove that the distance of the cloud from the point of observation is `(2h sec alpha)/(tan beta - tan alpha)`
A tower subtends an angle 𝛼 at a point A in the plane of its base and the angle if depression of the foot of the tower at a point b metres just above A is β. Prove that the height of the tower is b tan α cot β
A man is standing on the deck of a ship, which is 40 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill `(sqrt(3) = 1.732)`
There are two windows in a house. A window of the house is at a height of 1.5 m above the ground and the other window is 3 m vertically above the lower window. Ram and Shyam are sitting inside the two windows. At an instant, the angle of elevation of a balloon from these windows is observed as 45° and 30° respectively. Find the height of the balloon from the ground.
Lakshaman Jhula is located 5 kilometers north-east of the city of Rishikesh in the Indian state of Uttarakhand. The bridge connects the villages of Tapovan to Jonk. Tapovan is in Tehri Garhwal district, on the west bank of the river, while Jonk is in Pauri Garhwal district, on the east bank. Lakshman Jhula is a pedestrian bridge also used by motorbikes. It is a landmark of Rishikesh. A group of Class X students visited Rishikesh in Uttarakhand on a trip. They observed from a point (P) on a river bridge that the angles of depression of opposite banks of the river are 60° and 30° respectively. The height of the bridge is about 18 meters from the river. |
Based on the above information answer the following questions.
- Find the distance PA.
- Find the distance PB
- Find the width AB of the river.
[OR]
Find the height BQ if the angle of the elevation from P to Q be 30°.
An aeroplane when flying at a height of 3125 m from the ground passes vertically below another plane at an instant when the angles of elevation of the two planes from the same point on the ground are 30° and 60° respectively. Find the distance between the two planes at that instant.
