Advertisements
Advertisements
प्रश्न
From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
From the top of a 7 m high building, the angle of elevation of the top of a tower is 60° and the angle of depression of its foot is 45°. Find the height of the tower.
उत्तर १
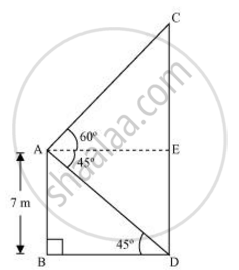
Let AB be a building and CD be a cable tower.
In ΔABD,
`"AB"/"BD"` = tan 45°
`7/"BD"` = 1
BD = 7 m
In ΔACE,
AE = BD = 7 m
`"CE"/"AE"` = tan 60°
`"CE"/7 = sqrt3`
`"CE" = 7sqrt3 "m"`
CD = CE + ED
= `(7sqrt3 + 7)"m"`
= `7(sqrt3 + 1)"m"`
Therefore, the height of the cable tower is `7(sqrt3+1)"m"`.
उत्तर २
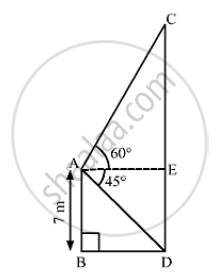
Let AB be the 7m high building and CD be the cable tower,
We have,
AB = 7 m, ∠CAE = 60°, ∠DAE = ∠ADB = 45°
Also, DE = AB = 7 m
In ΔABD,
tan 45° = `("AB")/("BD")`
⇒ 1 = `7/("BD")`
⇒ BD = 7 m
So, AE = BD = 7m
Also, In ΔACE,
tan 60° = `("CF")/("AE")`
⇒ `sqrt(3) = ("CE")/7`
⇒ CE = `7sqrt(3)"m"`
Now, CD = CE + DE
= `7 sqrt(3) +7`
= `7 (sqrt(3) +1) "m"`
= 7(1.732 + 1)
= 7(2.732)
= 19.124
= 19.12 m
So, the height of the tower is 19.12 m.
APPEARS IN
संबंधित प्रश्न
A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.

A contractor plans to install two slides for the children to play in a park. For the children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m, and is inclined at an angle of 30° to the ground, where as for the elder children, she wants to have a steep side at a height of 3 m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m. from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
On a straight line passing through the foot of a tower, two points C and D are at distances of 4 m and 16 m from the foot respectively. If the angles of elevation from C and D of the top of the tower are complementary, then find the height of the tower.
A man observes a car from the top of a tower, which is moving towards the tower with a uniform speed. If the angle of depression of the car changes from 30° to 45° in 12 minutes, find the time taken by the car now to reach the tower.
On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 150 m, find the distance between the objects.
A man standing on the deck of a ship, which is 8 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill.
A boy is standing on the ground and flying a kite with 100 m of string at an elevation of 30°. Another boy is sanding on the roof of a 10 m high building and is flying his kite at an elevation of 45°. Both the boys are on opposite sides of both the kites. Find the length of the string that the second boy must have so that the two kites meet.
A ladder 15 m long makes an angle of 60° with the wall. Find the height of the point where the ladder touches the wall.
A vertical tower stands on a horizontal plane and is surmounted by a flagstaff of height 5 m. From a point on the ground the angles of elevation of the top and bottom of the flagstaff are 60° and 30° respectively. Find the height of the tower and the distance of the point from the tower. (take\[\sqrt{3}\]= 1.732)
A kite is flying at a height of 45 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is
60°. Find the length of the string assuming that there is no slack in the string.
A kite is flying at a height of 60 m above the ground. The string attached to the kite is tied at the ground. It makes an angle of 60° with the ground. Assuming that the string is straight, find the length of the string.
In the following figure, what are the angles of depression from the observing position O1 and O2of the object at A?
If the angles of elevation of the top of a tower from two points distant a and b from the base and in the same straight line with it are complementary, then the height of the tower is
The angle of elevation of a cloud from a point h metre above a lake is θ. The angle of depression of its reflection in the lake is 45°. The height of the cloud is
The tops of two poles of height 16 m and 10 m are connected by a wire of length lmetres. If the wire makes an angle of 30° with the horizontal, then l =
An aeroplane is flying parallel to the Earth’s surface at a speed of 175 m/sec and at a height of 600 m. The angle of elevation of the aeroplane from a point on the Earth’s surface is 37°. After what period of time does the angle of elevation increase to 53°? (tan 53° = 1.3270, tan 37° = 0.7536)
In given figure, the value of AE is ____________.
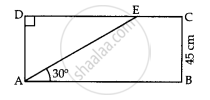
In figure given ABCD is a rectangle, the value of CE is ____________.

Two vertical poles of different heights are standing 20m away from each other on the level ground. The angle of elevation of the top of the first pole from the foot of the second pole is 60° and angle of elevation of the top of the second pole from the foot of the first pole is 30°. Find the difference between the heights of two poles. (Take `sqrt(3)` = 1.73)
