Advertisements
Advertisements
प्रश्न
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m. from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
उत्तर १
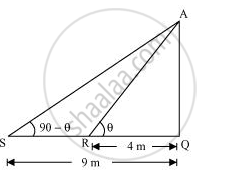
Let AQ be the tower and R, S are the points 4m, 9m away from the base of the tower respectively.
The angles are complementary. Therefore, if one angle is θ, the other will be 90 − θ.
In ΔAQR,
AQ/QR = tanΘ
AQ/4 = tanΘ ... 1
In ΔAQS,
AQ/SQ = tan(90 - Θ)
AQ/9 = cot Θ ...2
On multiplying equations (i) and (ii), we obtain
(AQ/4)(AQ/9) = (tanΘ).(cot Θ)
`(AQ^2)/36 = 1`
`AQ^2 = 36`
`AQ = sqrt36 = +-6`
However, height cannot be negative.
Therefore, the height of the tower is 6 m
उत्तर २
Let AB be the tower and C and D be two points such that AC = 4m and AD 9m.
Let:
`AB = hm, ∠BCA=theta and ∠BDA= 90° - theta`
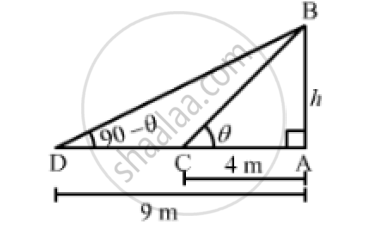
In the right ΔBCA,we have:
`tan theta = (AB)/(AC)`
`⇒ tan theta = h/4 ` ...............(1)
In the right ΔBDA,we have:
` tan (90° - theta ) = (AB) /(AD)`
`⇒ cot theta = h/9 [ tan (90° - theta ) = cot theta]`
`⇒1/ tan theta = h/9 ................(2) [ cot theta = 1/ tan theta]`
Multiplying equations (1) and (2), we get
`tan theta xx 1/ tan theta = h/4xxh/9`
`⇒ 1=( h^2)/36`
`⇒ 36=h^2`
`⇒h = +-6`
Height of a tower cannot be negative
∴Height of the tower = 6 m
संबंधित प्रश्न
A bus travels at a certain average speed for a distance of 75 km and then travels a distance of 90 km at an average speed of 10 km/h more than the first speed. If it takes 3 hours to complete the total journey, find its first speed?
A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground, making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
A TV tower stands vertically on a bank of a river/canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From a point 20 m away this point on the same bank, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the river/canal.
The angle of elevation of the top of a tower from ta point on the same level as the foot of the tower is 30° . On advancing 150 m towards foot of the tower, the angle of elevation becomes 60° Show that the height of the tower is 129.9 metres.
A person is standing at a distance of 80 m from a church looking at its top. The angle of elevation is of 45°. Find the height of the church.
Two poles are 'a' metres apart and the height of one is double of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the smaller is
Two ships are sailing in the sea on either side of the lighthouse. The angles of depression of two ships as observed from the top of the lighthouse are 60° and 45° respectively. If the distance between the ships is `200[(sqrt(3) + 1)/sqrt(3)]` metres, find the height of the lighthouse.
A building and a statue are in opposite side of a street from each other 35 m apart. From a point on the roof of building the angle of elevation of the top of statue is 24° and the angle of depression of base of the statue is 34°. Find the height of the statue. (tan 24° = 0.4452, tan 34° = 0.6745)
The angles of elevation of the top of the rock from the top and foot of 100 m high tower are respectively 30° and 45°. The height of the rock is ____________.
The angle of elevation of the top of a tower from two points distant s and t from its foot are complementary. Prove that the height of the tower is `sqrt(st)`
