Question

The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m. from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.

Answer 1

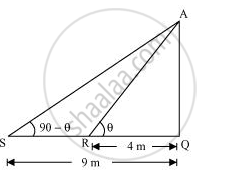
Let AQ be the tower and R, S are the points 4m, 9m away from the base of the tower respectively.

The angles are complementary. Therefore, if one angle is θ, the other will be 90 − θ.

In ΔAQR,

AQ/QR = tanΘ  

AQ/4 = tanΘ    ... 1

In ΔAQS,

AQ/SQ = tan(90 - Θ)

AQ/9 = cot Θ ...2

On multiplying equations (i) and (ii), we obtain

(AQ/4)(AQ/9) = (tanΘ).(cot Θ)

`(AQ^2)/36 = 1`

`AQ^2 = 36`

`AQ = sqrt36 = +-6`

However, height cannot be negative.

Therefore, the height of the tower is 6 m

Answer 2

Let AB be the tower and C and D be two points such that AC = 4m and AD  9m.
Let:
`AB = hm, ∠BCA=theta  and ∠BDA=  90° - theta`

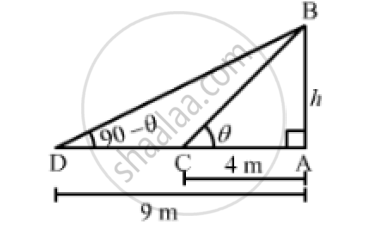
In the right ΔBCA,we have:

`tan theta = (AB)/(AC)`

`⇒ tan theta = h/4 `           ...............(1)

In the right  ΔBDA,we have:

` tan (90° - theta ) = (AB) /(AD)`

`⇒ cot theta = h/9                     [ tan (90° - theta ) = cot theta]`

`⇒1/ tan theta = h/9            ................(2)       [ cot theta = 1/ tan theta]`

Multiplying equations (1) and (2), we get

`tan theta xx 1/ tan theta = h/4xxh/9`

`⇒ 1=( h^2)/36`

`⇒ 36=h^2`

`⇒h = +-6`

 Height of a tower cannot be negative
∴Height of the tower = 6 m