Advertisements
Advertisements
प्रश्न
At a point on level ground, the angle of elevation of a vertical tower is, found to be α such that tan α = `1/3`. After walking 100 m towards the tower, the angle of elevation β becomes such that tan β = `3/4`. Find the height of the tower.
उत्तर
Let the height of the tower be h m.
Given, tan α = `1/3` and tan β = `3/4`
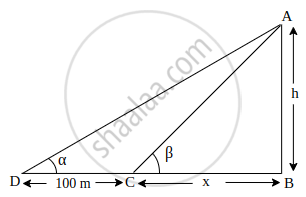
Now, In ΔABD, ∠D = α, ∠B = 90°
tan α = `("AB")/("DB")`
⇒ `1/3 = "h"/(100 + x)`
⇒ 100 + x = 3h
⇒ x = 3h – 100 ...(i)
In ΔABC, ∠C = β, ∠B = 90°
tan β = `("AB")/("BC")`
⇒ `3/4 = "h"/x`
⇒ x = `(4"h")/3` ...(ii)
From equations (i) and (ii), we have
3h – 100 = `(4"h")/3`
⇒ `3"h" - (4"h")/3` = 100
⇒ `(5"h")/3` = 100
⇒ h = `300/5`
⇒ h = 60 m
Hence, the height of the tower is 60 m.
APPEARS IN
संबंधित प्रश्न
From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower. (Use `sqrt3` = 1.73)
A vertically straight tree, 15 m high, is broken by the wind in such a way that its top just touches the ground and makes an angle of 60° with the ground. At what height from the ground did the tree break?
On a horizontal plane, there is a vertical tower with a flagpole on the top of the tower. At a point 9 meters away from the foot of the tower the angle of elevation of the top and bottom of the flagpole are 60° and 30° respectively. Find the height of the tower and the flagpole mounted on it.
From a point P on the ground the angle of elevation of a 10 m tall building is 30°. A flag is hoisted at the top of the building and the angle of elevation of the top of the flag-staff from P is 45°. Find the length of the flag-staff and the distance of the building from the point P. (Take `sqrt3` = 1.732)
A kite is flying at a height of 30 m from the ground. The length of string from the kite to the ground is 60 m. Assuming that there is no slack in the string, the angle of elevation of the kite at the ground is
The tops of two poles of height 16 m and 10 m are connected by a wire of length lmetres. If the wire makes an angle of 30° with the horizontal, then l =
The height of the vertical pole is \[\sqrt{3}\] times the length of its shadow on the ground, then angle of elevation of the sun at that time is
The angle of elevation of the top of a tower 30 m high from the foot of another tower in the same plane is 60°, then the distance between the two towers is ____________.
There are two windows in a house. A window of the house is at a height of 1.5 m above the ground and the other window is 3 m vertically above the lower window. Ram and Shyam are sitting inside the two windows. At an instant, the angle of elevation of a balloon from these windows is observed as 45° and 30° respectively. Find the height of the balloon from the ground.
Two vertical poles AB = 15 m and CD = 10 m are standing apart on a horizontal ground with points A and C on the ground. If P is the point of intersection of BC and AD, then the height of P (in m) above the line AC is ______.
