Advertisements
Advertisements
प्रश्न
From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower. (Use `sqrt3` = 1.73)
From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.
उत्तर १

Let AB be the building of height 20 m and BC the transmission tower of height h meter.
∴ AB = 20 m
∴ BC = h m
O is the point of observation.
Let the angle of elevation of the bottom and top of the tower at the point o is 45° and 60° respectively.
∴ ∠COA = 60° and ∠BOA = 45°
In ΔOAB,
tan∠BOA = `"AB"/"AO"`
∴ tan 45° = `20/x`
∴ 1 = `20/x`
∴ x = 20 m
∴ AO = 20 m ...(1)
In ΔOAC,
tan ∠COA = `"AC"/"AO"`
tan 60° = `"AB + BC"/"AO"`
`sqrt3 = (20 + h)/20`
20`sqrt3` = 20 + h
∴ h = 20`sqrt3` − 20
∴ h = 20(`sqrt3` − 1)
Here, `sqrt3` = 1.73 ...(Given)
∴ h = 20(1.73 − 1)
∴ h = 20 × 0.73
∴ h = 14.64 m
Height of tower (h) = 14.64 m.
उत्तर २

Let AB be the building of height 20 m and BC the transmission tower of height h meter.
∴ AB = 20 m
∴ BC = h m
O is the point of observation. Let the angle of elevation of the bottom and top of the tower at the point o be 45° and 60°, respectively.
∴ ∠COA = 60° and ∠BOA = 45°
In ΔOAB,
tan∠BOA = `"AB"/"AO"`
∴ tan 45° = `20/x`
∴ 1 = `20/x`
∴ x = 20 m
∴ AO = 20 m ...(1)
In ΔOAC,
tan ∠COA = `"AC"/"AO"`
tan 60° = `"AB + BC"/"AO"`
`sqrt3 = (20 + h)/20`
20`sqrt3` = 20 + h
∴ h = 20`sqrt3` − 20
∴ h = 20(`sqrt3` − 1)
h = 20 × 0.732
h = 14.64
Thus, the height of the tower is 14.64 m.
APPEARS IN
संबंधित प्रश्न
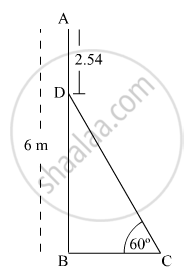
In Fig. 1, AB is a 6 m high pole and CD is a ladder inclined at an angle of 60° to the horizontal and reaches up to a point D of pole. If AD = 2.54 m, find the length of the ladder. (use3√=1.73)
An aeroplane when flying at a height of 4000m from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60º and 45º respectively. Find the vertical distance between the aeroplanes at that instant
As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
A parachutist is descending vertically and makes angles of elevation of 45° and 60° at two observing points 100 m apart from each other on the left side of himself. Find the maximum height from which he falls and the distance of the point where he falls on the ground form the just observation point.
A carpenter makes stools for electricians with a square top of side 0.5 m and at a height of 1.5 m above the ground. Also, each leg is inclined at an angle of 60° to the ground. Find the length of each leg and also the lengths of two steps to be put at equal distances.
A kite is flying at a height of 75 in from the level ground, attached to a string inclined at 60°. to the horizontal. Find the length of the string, assuming that there is no slack in it.
[Take `sqrt(3)` =1.732 ]
From the point of a tower 100m high, a man observe two cars on the opposite sides to the tower with angles of depression 30° and 45 respectively. Find the distance between the cars
The shadow of a tower at a time is three times as long as its shadow when the angle of elevation of the sun is 60°. Find the angle of elevation of the sun at the time of the longer shadow ?
If the height of a vertical pole is 3–√3 times the length of its shadow on the ground, then the angle of elevation of the Sun at that time is
(A) 30°
(B) 60°
(C) 45°
(D) 75°

Radii of the top and the base of a frustum of a cone are 5 cm and 2 cm respectively. Its height is 9 cm. Find its volume. (π = 3.14)
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30° with horizontal, then the length of the wire is
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 84 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
Find the distance between the points (a, b) and (−a, −b).
The angle of depression of the top and bottom of 20 m tall building from the top of a multistoried building are 30° and 60° respectively. The height of the multistoried building and the distance between two buildings (in metres) is
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is C to the North of B?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
If two towers of heights h1 and h2 subtend angles of 60° and 30° respectively at the mid-point of the line joining their feet, then h1: h2 = ____________.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
As observed from the top of a 150 m high lighthouse from the sea level, the angles of depression of the two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships.
A tower stands vertically on the ground. From a point on the ground, which is 30 m away from the foot of the tower, the angle of elevation of the top of the tower is found to be 30°. Find the height of the tower.
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun is also increasing.
