Advertisements
Advertisements
प्रश्न
A carpenter makes stools for electricians with a square top of side 0.5 m and at a height of 1.5 m above the ground. Also, each leg is inclined at an angle of 60° to the ground. Find the length of each leg and also the lengths of two steps to be put at equal distances.
उत्तर
Let the length of stool,AB = 0.5 m, height AC = 1.5 m and its leg inclined at an angle of 60° to the ground.
Let the length of leg AE = hm

We have to find the length of leg, lengths of two steps equal in length.
in ΔAEC, ∠AEC = 60°
`sin 60° = (AC)/(AE)`
`=> sqrt3/2 = 1.5/h`
`=> h = 3/sqrt3`
=> h = 1.732
In ΔAGH, ∠AGH = 60° and AH = 0.5 m
`tan 60^@ = (AH)/(GH)`
`=> sqrt3 = 0.5/GH`
`=> GH = 0.5/sqrt3`
`=> GH = 0.2886`
Total length = `0.5 + (0.2886 xx 2) = 1.1077 m`
In Δ APQ, ∠APQ = 60° and AQ = 1 m
`tan 60^@ = (AQ)/(PQ)`
`=> sqrt3 = 1/Pq`
`=> PQ = 1/sqrt3`
=> PQ = 0.577
Total lengths 0.5 + (0.577 x 2) = 1.654 m
Hence the length of leg is 1.732 m
And length of eacb are 1.1077 m and 1.654 m
APPEARS IN
संबंधित प्रश्न
From the top of a lighthouse, the angles of depression of two ships on the opposite sides of it are observed to be a and 3. If the height of the lighthouse be h meters and the line joining the ships passes through the foot of the lighthouse, show that the distance
`(h(tan alpha + tan beta))/(tan alpha tan beta)` meters
Two buildings are facing each other on a road of width 12 metre. From the top of the first building, which is 10 metre high, the angle of elevation of the top of the second is found to be 60°. What is the height of the second building ?

Radii of the top and the base of a frustum of a cone are 5 cm and 2 cm respectively. Its height is 9 cm. Find its volume. (π = 3.14)
In the following figure, what are the angles of depression from the observing position O1 and O2of the object at A?
The angles of depression of two ships from the top of a light house are 45° and 30° towards east. If the ships are 100 m apart. the height of the light house is
A tower subtends an angle of 30° at a point on the same level as its foot. At a second point h metres above the first, the depression of the foot of the tower is 60°. The height of the tower is
To a man standing outside his house, the angles of elevation of the top and bottom of a window are 60° and 45° respectively. If the height of the man is 180 cm and if he is 5 m away from the wall, what is the height of the window? `(sqrt(3) = 1.732)`
At some time of the day, the length of the shadow of a tower is equal to its height. Then, the sun’s altitude at that time is ______.
If the length of the shadow of a tower is increasing, then the angle of elevation of the sun ____________.
|
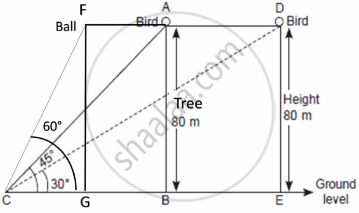
One evening, Kaushik was in a park. Children were playing cricket. Birds were singing on a nearby tree of height 80m. He observed a bird on the tree at an angle of elevation of 45°. When a sixer was hit, a ball flew through the tree frightening the bird to fly away. In 2 seconds, he observed the bird flying at the same height at an angle of elevation of 30° and the ball flying towards him at the same height at an angle of elevation of 60°.
|
- At what distance from the foot of the tree was he observing the bird sitting on the tree?
- How far did the bird fly in the mentioned time?
(or)
After hitting the tree, how far did the ball travel in the sky when Kaushik saw the ball? - What is the speed of the bird in m/min if it had flown `20(sqrt3 + 1) m`?