Advertisements
Advertisements
प्रश्न
The angles of depression of two ships from the top of a light house are 45° and 30° towards east. If the ships are 100 m apart. the height of the light house is
पर्याय
\[\frac{50}{\sqrt{3 + 1}} m\]
\[\frac{50}{\sqrt{3 - 1}} m\]
\[50 \left( \sqrt{3} - 1 \right) m\]
\[50 \left( \sqrt{3} + 1 \right) m\]
उत्तर
Let AB= h be the light house.
The given situation can be represented as,
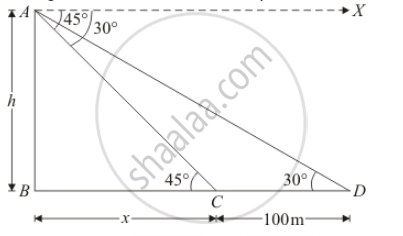
It is clear that`∠C=45°` and `∠D=30°`
Again, let`BC=x` and`CD=100` m is given.
Here, we have to find the height of light house.
So we use trigonometric ratios.
In a triangle,`ABC`
`⇒ tan C=AB/BC`
`⇒ tan 45°=h/x`
`⇒ 1=h/x`
`⇒h=x`
Again in a triangle ABD,
`⇒ tan D=(AB)/(BC+CD)`
`⇒ tan 30°= h/(x+100)`
`⇒1/sqrt3=h/(x+100)`
`⇒sqrt3h=x+100`
Put `x=h`
`⇒ sqrt3h=h+100`
`⇒ h(sqrt3-1)=100`
`⇒h=100/(sqrt3-1)=100`
`⇒ h=100/(sqrt3-1)`
`⇒ h=100/(sqrt3-1) xx (sqrt3+1)/(sqrt3+1)`
`⇒ h=50(sqrt3+1)`
APPEARS IN
संबंधित प्रश्न
If a vertical pole 6m high has a shadow of length 2 √3 metres, find the angle of elevation of the sun.
A balloon is connected to a meteorological station by a cable of length 200 m, inclined at 60º to the horizontal. Find the height of the balloon from the ground. Assume that there is no slack in the cable
A parachutist is descending vertically and makes angles of elevation of 45° and 60° at two observing points 100 m apart from each other on the left side of himself. Find the maximum height from which he falls and the distance of the point where he falls on the ground form the just observation point.
The horizontal distance between two poles is 15 m. The angle of depression of the top of first pole as seen from the top of second pole is 30°. If the height of the second pole is 24 m, find the height of the first pole. Use`[sqrt3=1.732]`
From the top of the light house, an observer looks at a ship and finds the angle of depression to be 30°. If the height of the light-house is 100 meters, then find how far the ship is from the light-house.
The angle of elevation of the top of a tower at a point on the ground is 30º. What will be the angle of elevation, if the height of the tower is tripled?
The angles of elevation of the top of the rock from the top and foot of 100 m high tower are respectively 30° and 45°. The height of the rock is ____________.
A ladder 15 meters long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then the height of the wall will be ____________.
A ladder 15 metres long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, find the height of the wall.
Read the following passage and answer the questions given below.
|
Qutub Minar, located in South Delhi, India was built in the year 1193. It is 72 m high tower. Working on a school project, Charu and Daljeet visited the monument. They used trigonometry to find their distance from the tower. Observe the picture given below. Points C and D represent their positions on the ground in line with the base of tower, the angles of elevation of top of the tower (Point A) are 60° and 45° from points C and D respectively.
|
- Based on the above information, draw a well-labelled diagram.
- Find the distances CD, BC and BD. [use `sqrt(3)` = 1.73]

