Advertisements
Advertisements
Question
The angles of depression of two ships from the top of a light house are 45° and 30° towards east. If the ships are 100 m apart. the height of the light house is
Options
\[\frac{50}{\sqrt{3 + 1}} m\]
\[\frac{50}{\sqrt{3 - 1}} m\]
\[50 \left( \sqrt{3} - 1 \right) m\]
\[50 \left( \sqrt{3} + 1 \right) m\]
Solution
Let AB= h be the light house.
The given situation can be represented as,
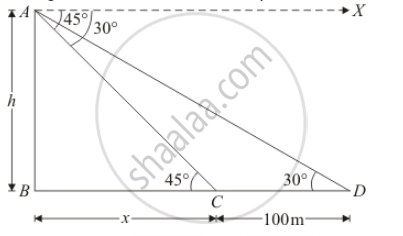
It is clear that`∠C=45°` and `∠D=30°`
Again, let`BC=x` and`CD=100` m is given.
Here, we have to find the height of light house.
So we use trigonometric ratios.
In a triangle,`ABC`
`⇒ tan C=AB/BC`
`⇒ tan 45°=h/x`
`⇒ 1=h/x`
`⇒h=x`
Again in a triangle ABD,
`⇒ tan D=(AB)/(BC+CD)`
`⇒ tan 30°= h/(x+100)`
`⇒1/sqrt3=h/(x+100)`
`⇒sqrt3h=x+100`
Put `x=h`
`⇒ sqrt3h=h+100`
`⇒ h(sqrt3-1)=100`
`⇒h=100/(sqrt3-1)=100`
`⇒ h=100/(sqrt3-1)`
`⇒ h=100/(sqrt3-1) xx (sqrt3+1)/(sqrt3+1)`
`⇒ h=50(sqrt3+1)`
APPEARS IN
RELATED QUESTIONS
At a point A, 20 metres above the level of water in a lake, the angle of elevation of a cloud is 30˚. The angle of depression of the reflection of the cloud in the lake, at A is 60˚.
Find the distance of the cloud from A.
An aeroplane when flying at a height of 4000m from the ground passes vertically above another aeroplane at an instant when the angles of the elevation of the two planes from the same point on the ground are 60º and 45º respectively. Find the vertical distance between the aeroplanes at that instant
On the same side of a tower, two objects are located. When observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 150 m, find the distance between the objects.
A ladder 15 m long makes an angle of 60° with the wall. Find the height of the point where the ladder touches the wall.
A tower subtends an angle of 30° at a point on the same level as its foot. At a second point h metres above the first, the depression of the foot of the tower is 60°. The height of the tower is
An aeroplane at an altitude of 1800 m finds that two boats are sailing towards it in the same direction. The angles of depression of the boats as observed from the aeroplane are 60° and 30° respectively. Find the distance between the two boats. `(sqrt(3) = 1.732)`
If at some time, the length of the shadow of a tower is `sqrt3` times its height, then the angle of elevation of the sun, at that time is ____________.
A vertical pole of 30 m is fixed on a tower. From a point on the level ground, the angle of elevation of the top and bottom of the pole is 60° and 45°. Find the height of the tower.
If the height of a tower and the distance of the point of observation from its foot, both, are increased by 10%, then the angle of elevation of its top remains unchanged.
|
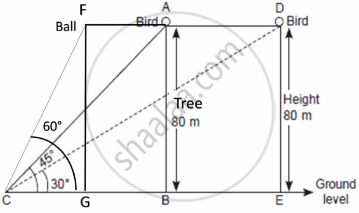
One evening, Kaushik was in a park. Children were playing cricket. Birds were singing on a nearby tree of height 80m. He observed a bird on the tree at an angle of elevation of 45°. When a sixer was hit, a ball flew through the tree frightening the bird to fly away. In 2 seconds, he observed the bird flying at the same height at an angle of elevation of 30° and the ball flying towards him at the same height at an angle of elevation of 60°.
|
- At what distance from the foot of the tree was he observing the bird sitting on the tree?
- How far did the bird fly in the mentioned time?
(or)
After hitting the tree, how far did the ball travel in the sky when Kaushik saw the ball? - What is the speed of the bird in m/min if it had flown `20(sqrt3 + 1) m`?