Advertisements
Advertisements
Question
From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. The height of the tower is
Options
25 m
50 m
75 m
100 m
Solution
Given that: height of cliff is 25 m and angle of elevation of the tower is equal to angle of depression of foot of the tower that is θ.
Now, the given situation can be represented as,
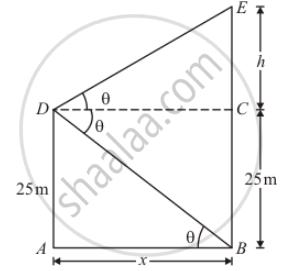
Here, D is the top of cliff and BE is the tower.
Let CE = h, `AB=x`. Then, `AB=DC`= = x
Here, we have to find the height of the tower BE.
So, we use trigonometric ratios.
In a triangle ABD,
`⇒ tan θ= AD/AB`
`⇒ tan θ=25/x` (1)
Again in a triangle,`DCE`
`tan θ=(CE)/(CD)`
`⇒ tan θ=h/x`
`⇒25/x=h/x` [using 1]
`⇒h=25`
Thus, height of the tower = BE = BC + CE = (25 + 25) m = 50 m
APPEARS IN
RELATED QUESTIONS
The angle of elevation of the top of a tower from a point A due south of the tower is α and from B due east of the tower is β. If AB = d, show that the height of the tower is
`\frac{d}{\sqrt{\cot ^{2}\alpha +\cot^{2}\beta `
Two poles of equal heights are standing opposite each other an either side of the road, which is 80 m wide. From a point between them on the road, the angles of elevation of the top of the poles are 60° and 30º, respectively. Find the height of poles and the distance of the point from the poles.
The angles of elevation of the top of a tower from two points at distance of 5 metres and 20 metres from the base of the tower and is the same straight line with it, are complementary. Find the height of the tower.
From a point on the ground 40m away from the foot of a tower, the angle of elevation of the top of the tower is 30 . The angle of elevation of the top of a water tank (on the top of the tower) is 45 , Find (i) the height of the tower, (ii) the depth of the tank.
From a light house the angles of depression of two ships on opposite sides of the light house are observed to be 30° and 45°. If the height of the light house is h metres, the distance between the ships is
Two poles are 'a' metres apart and the height of one is double of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the smaller is
The angle of elevation of the top of a tower at a point on the ground 50 m away from the foot of the tower is 45º. Then the height of the tower (in metres) is
If the ratio of the height of a tower and the length of its shadow is `sqrt(3): 1`, then the angle of elevation of the sun has measure
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
Two circles of radii 5 cm and 3 cm touch each other externally. Find the distance between their centres.
