Advertisements
Advertisements
प्रश्न
From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. The height of the tower is
पर्याय
25 m
50 m
75 m
100 m
उत्तर
Given that: height of cliff is 25 m and angle of elevation of the tower is equal to angle of depression of foot of the tower that is θ.
Now, the given situation can be represented as,
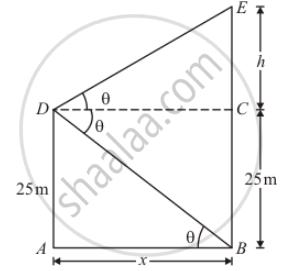
Here, D is the top of cliff and BE is the tower.
Let CE = h, `AB=x`. Then, `AB=DC`= = x
Here, we have to find the height of the tower BE.
So, we use trigonometric ratios.
In a triangle ABD,
`⇒ tan θ= AD/AB`
`⇒ tan θ=25/x` (1)
Again in a triangle,`DCE`
`tan θ=(CE)/(CD)`
`⇒ tan θ=h/x`
`⇒25/x=h/x` [using 1]
`⇒h=25`
Thus, height of the tower = BE = BC + CE = (25 + 25) m = 50 m
APPEARS IN
संबंधित प्रश्न
At a point A, 20 metres above the level of water in a lake, the angle of elevation of a cloud is 30˚. The angle of depression of the reflection of the cloud in the lake, at A is 60˚.
Find the distance of the cloud from A.
The pilot of a helicopter, at an altitude of 1200m finds that the two ships are sailing towards it in the same direction. The angle of depression of the ships as observed from the helicopter are 60º and 45º respectively. Find the distance between the two ships
A straight highway leads to the foot of a tower of height 50 m. From the top of the tower, the angles of depression of two cars standing on the highway are 30° and 60° respectively. What is the distance the two cars and how far is each car from the tower?
From the top of the light house, an observer looks at a ship and finds the angle of depression to be 30°. If the height of the light-house is 100 meters, then find how far the ship is from the light-house.

Radii of the top and the base of a frustum of a cone are 5 cm and 2 cm respectively. Its height is 9 cm. Find its volume. (π = 3.14)
If two circles having centers P and Q and radii 3 cm and 5 cm. touch each other externally, find the distance PQ.
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find the height of the lamp post
A plane is observed to be approaching the airport. It is at a distance of 12 km from the point of observation and makes an angle of elevation of 60°. The height above the ground of the plane is ____________.
If two towers of heights h1 and h2 subtend angles of 60° and 30° respectively at the mid-point of the line joining their feet, then h1: h2 = ____________.
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 60 m high, find the height of the building.
