Advertisements
Advertisements
प्रश्न
From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. The height of the tower is
विकल्प
25 m
50 m
75 m
100 m
उत्तर
Given that: height of cliff is 25 m and angle of elevation of the tower is equal to angle of depression of foot of the tower that is θ.
Now, the given situation can be represented as,
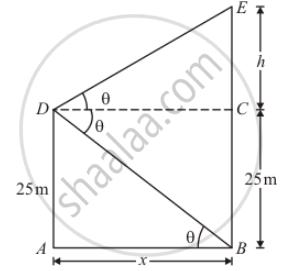
Here, D is the top of cliff and BE is the tower.
Let CE = h, `AB=x`. Then, `AB=DC`= = x
Here, we have to find the height of the tower BE.
So, we use trigonometric ratios.
In a triangle ABD,
`⇒ tan θ= AD/AB`
`⇒ tan θ=25/x` (1)
Again in a triangle,`DCE`
`tan θ=(CE)/(CD)`
`⇒ tan θ=h/x`
`⇒25/x=h/x` [using 1]
`⇒h=25`
Thus, height of the tower = BE = BC + CE = (25 + 25) m = 50 m
APPEARS IN
संबंधित प्रश्न
The tops of two towers of height x and y, standing on level ground, subtend angles of 30° and 60° respectively at the centre of the line joining their feet, then find x, y.
A ladder against a vertical wall makes an angle of 45º with the ground. The foot of the ladder is 3m from the wall. Find the length of the ladder
Two stations due south of a leaning tower which leans towards the north are at distance a and b from its foot. If α, β be the elevations of the top of the tower from these stations, prove that its inclination θ to the horizontal is given by `\text{cot }\theta =\frac{bcot alpha -a\cot \beta }{b-a}`
There are two temples, one on each bank of a river, just opposite to each other. One temple is 50 m high. From the top of this temple, the angles of depression of the top and the foot of the other temple are 30° and 60° respectively. Find the width of the river and the height of the other temple.
A pole casts a shadow of length \[2\sqrt{3}\] m on the ground, when the sun's elevation is 60°. Find the height of the pole.
The angle of depression of a car, standing on the ground, from the top of a 75 m high tower, is 30°. The distance of the car from the base of the tower (in m.) is:
From the top of a lighthouse, an observer looks at a ship and finds the angle of depression to be 60° . If the height of the lighthouse is 84 meters, then find how far is that ship from the lighthouse? (√3 = 1.73)
A bird is flying from A towards B at an angle of 35°, a point 30 km away from A. At B it changes its course of flight and heads towards C on a bearing of 48° and distance 32 km away. How far is C to the North of B?
(sin 55° = 0.8192, cos 55° = 0.5736, sin 42° = 0.6691, cos 42° = 0.7431)
The angle of elevation of the top of a tower from a point 20 meters away from its base is 45°. The height of the tower is ____________.
A vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flagstaff are α and β, respectively. Then the height of the tower is ____________.
