Advertisements
Advertisements
प्रश्न
The angle of depression of a car, standing on the ground, from the top of a 75 m high tower, is 30°. The distance of the car from the base of the tower (in m.) is:
विकल्प
(A)`25sqrt3`
(B)`50sqrt3`
(C)`75sqrt3`
(D) 150
उत्तर
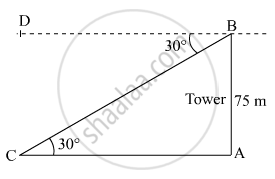
Let AB be the tower of height 75 m.
∠ABD = ∠ACB = 30°
Suppose C be the position of the car from the base of the tower.
In right ΔABC,
`cot 30^o=(AC)/(AB)`
`rArrAC=AB\ cot30^o`
`rArrAC=75mxxsqrt3`
`rArrAC=75sqrt3 m`
Thus, the distance of the car from the base of the tower is `75sqrt3m`.
संबंधित प्रश्न
The angle of elevation of a cliff from a fixed point is θ. After going up a distance of k metres towards the top of cliff at an angle of φ, it is found that the angle of elevation is α. Show that the height of the cliff is metres
The shadow of a tower, when the angle of elevation of the sun is 45°, is found to be 10 m. longer than when it was 600. Find the height of the tower.
Two boats approach a lighthouse in mid-sea from opposite directions. The angles of elevation of the top of the lighthouse from two boats are 30° and 45° respectively. If the distance between two boats is 100 m, find the height of the lighthouse.
Two men on either side of a 75 m high building and in line with base of building observe the angles of elevation of the top of the building as 30° and 60°. Find the distance between the two men. (Use\[\sqrt{3} = 1 . 73\])
If the angle of elevation of a tower from a distance of 100 metres from its foot is 60°, then the height of the tower is
A man in a boat rowing away from a lighthouse 100 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 30°.
Find the speed of the boat in metres per minute. [Use `sqrt(3` = 1.732]Use 3=1.732">
Find the angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of a tower of height `10sqrt(3)` m
Two poles are 25 m and 15 m high, and the line joining their tops makes an angle of 45° with the horizontal. The distance between these poles is ______.
The angle of elevation of the top of a tower from two points distant s and t from its foot are complementary. Prove that the height of the tower is `sqrt(st)`
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45°. If the bridge is at a height of 8 m from the banks, then find the width of the river.