Advertisements
Advertisements
प्रश्न
A man in a boat rowing away from a lighthouse 100 m high takes 2 minutes to change the angle of elevation of the top of the lighthouse from 60° to 30°.
Find the speed of the boat in metres per minute. [Use `sqrt(3` = 1.732]Use 3=1.732">
उत्तर
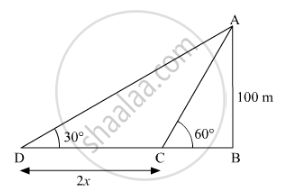
AB is a lighthouse of height 100m.
Let the speed of the boat be x metres per minute.
And CD is the distance which man travelled to change the angle of elevation.
So, CD = 2x ...[∵ Distance = Speed x Time]
tan (60°) = `("AB")/("BC")`
`sqrt(3) = (100)/("BC")`
⇒ `"BC" = (100)/(sqrt(3)`
tan (30°) = `("AB")/("BD")`
`(1)/sqrt(3) = (100)/("BD")`
`"BD" = 100 sqrt(3)`
`"CD"= "BD" - "BC"`
`2"x" = 100sqrt(3) - (100)/sqrt(3)`
`2"x" = (300-100)/sqrt(3)`
⇒ `"x" = (200)/(2sqrt(3)`
⇒ `"x" = (100)/(sqrt3)`
Using `sqrt(3)` = 1.73
`"x" = (100)/(1.73) ≈ 57.80`
Hence, the speed of the boat is 57.80">57.8057.80 metres per minute.
APPEARS IN
संबंधित प्रश्न
A passenger, while boarding the plane, slipped form the stairs and got hurt. The pilot took the passenger in the emergency clinic at the airport for treatment. Due to this, the plane got delayed by half an hour. To reach the destination 1500 km away in time, so that the passengers could catch the connecting flight, the speed of the plane was increased by 250 km/hour than the usual speed. Find the usual speed of the plane
What value is depicted in this question?
The shadow of a tower, when the angle of elevation of the sun is 45°, is found to be 10 m. longer than when it was 600. Find the height of the tower.
A kite is flying at a height of 75 in from the level ground, attached to a string inclined at 60°. to the horizontal. Find the length of the string, assuming that there is no slack in it.
[Take `sqrt(3)` =1.732 ]
The angle of depression of a car, standing on the ground, from the top of a 75 m tower, is 30°. The distance of the car from the base of the tower (in metres) is
A ladder 15 m long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, then the height of the wall is
A tree is broken by the wind. The top struck the ground at an angle of 30° and at a distance 30 m from the root. Find the whole height of the tree. (`sqrt(3)`=1.73)
If two towers of heights h1 and h2 subtend angles of 60° and 30° respectively at the mid-point of the line joining their feet, then h1: h2 = ____________.
A pole 6 m high casts a shadow `2sqrt(3)` m long on the ground, then the Sun’s elevation is ______.
Lakshaman Jhula is located 5 kilometers north-east of the city of Rishikesh in the Indian state of Uttarakhand. The bridge connects the villages of Tapovan to Jonk. Tapovan is in Tehri Garhwal district, on the west bank of the river, while Jonk is in Pauri Garhwal district, on the east bank. Lakshman Jhula is a pedestrian bridge also used by motorbikes. It is a landmark of Rishikesh. A group of Class X students visited Rishikesh in Uttarakhand on a trip. They observed from a point (P) on a river bridge that the angles of depression of opposite banks of the river are 60° and 30° respectively. The height of the bridge is about 18 meters from the river. |
Based on the above information answer the following questions.
- Find the distance PA.
- Find the distance PB
- Find the width AB of the river.
[OR]
Find the height BQ if the angle of the elevation from P to Q be 30°.
From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 3 m from the banks, find the width of the river. (Use `sqrt(3)` = 1.73)
